Samiksha Jaiswal (Editor)

Maxwell material

Updated on
Edit
Like
Comment
Share on FacebookTweet on TwitterShare on LinkedInShare on Reddit
Maxwell material

A Maxwell material is a viscoelastic material having the properties both of elasticity and viscosity. It is named for James Clerk Maxwell who proposed the model in 1867. It is also known as a Maxwell fluid.

Contents

Definition

The Maxwell model can be represented by a purely viscous damper and a purely elastic spring connected in series, as shown in the diagram. In this configuration, under an applied axial stress, the total stress, σ T o t a l and the total strain, ε T o t a l can be defined as follows:

σ T o t a l = σ D = σ S ε T o t a l = ε D + ε S

where the subscript D indicates the stress/strain in the damper and the subscript S indicates the stress/strain in the spring. Taking the derivative of strain with respect to time, we obtain:

d ε T o t a l d t = d ε D d t + d ε S d t = σ η + 1 E d σ d t

where E is the elastic modulus and η is the material coefficient of viscosity. This model describes the damper as a Newtonian fluid and models the spring with Hooke's law.

If we connect these two elements in parallel, we get a generalized model of Kelvin–Voigt material.

In a Maxwell material, stress σ, strain ε and their rates of change with respect to time t are governed by equations of the form:

1 E d σ d t + σ η = d ε d t

or, in dot notation:

σ ˙ E + σ η = ε ˙

The equation can be applied either to the shear stress or to the uniform tension in a material. In the former case, the viscosity corresponds to that for a Newtonian fluid. In the latter case, it has a slightly different meaning relating stress and rate of strain.

The model is usually applied to the case of small deformations. For the large deformations we should include some geometrical non-linearity. For the simplest way of generalizing the Maxwell model, refer to the upper-convected Maxwell model.

Effect of a sudden deformation

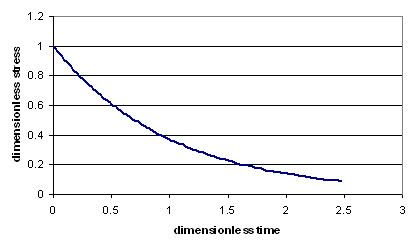
If a Maxwell material is suddenly deformed and held to a strain of ε 0 , then the stress decays with a characteristic time of η E .

The picture shows dependence of dimensionless stress σ ( t ) E ε 0 upon dimensionless time E η t :

If we free the material at time t 1 , then the elastic element will spring back by the value of

ε b a c k = − σ ( t 1 ) E = ε 0 exp ⁡ ( − E η t 1 ) .

Since the viscous element would not return to its original length, the irreversible component of deformation can be simplified to the expression below:

ε i r r e v e r s i b l e = ε 0 ( 1 − exp ⁡ ( − E η t 1 ) ) .

Effect of a sudden stress

If a Maxwell material is suddenly subjected to a stress σ 0 , then the elastic element would suddenly deform and the viscous element would deform with a constant rate:

ε ( t ) = σ 0 E + t σ 0 η

If at some time t 1 we would release the material, then the deformation of the elastic element would be the spring-back deformation and the deformation of the viscous element would not change:

ε r e v e r s i b l e = σ 0 E , ε i r r e v e r s i b l e = t 1 σ 0 η .

The Maxwell Model does not exhibit creep since it models strain as linear function of time.

If a small stress is applied for a sufficiently long time, then the irreversible strains become large. Thus, Maxwell material is a type of liquid.

Dynamic modulus

The complex dynamic modulus of a Maxwell material would be:

E ∗ ( ω ) = 1 1 / E − i / ( ω η ) = E η 2 ω 2 + i ω E 2 η η 2 ω 2 + E 2

Thus, the components of the dynamic modulus are :

E 1 ( ω ) = E η 2 ω 2 η 2 ω 2 + E 2 = ( η / E ) 2 ω 2 ( η / E ) 2 ω 2 + 1 E = τ 2 ω 2 τ 2 ω 2 + 1 E

and

E 2 ( ω ) = ω E 2 η η 2 ω 2 + E 2 = ( η / E ) ω ( η / E ) 2 ω 2 + 1 E = τ ω τ 2 ω 2 + 1 E

The picture shows relaxational spectrum for Maxwell material. The relaxation time constant is τ ≡ η / E .

References

Maxwell material Wikipedia
(Text) CC BY-SA