Suvarna Garge (Editor)

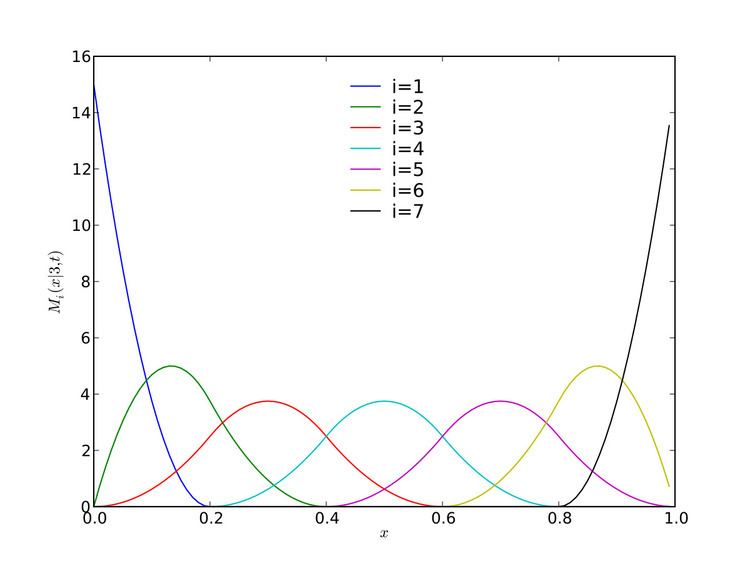
M spline

Updated on
Edit
Like
Comment
Share on FacebookTweet on TwitterShare on LinkedInShare on Reddit
M-spline

In the mathematical subfield of numerical analysis, an M-spline is a non-negative spline function.

Contents

Definition

A family of M-spline functions of order k with n free parameters is defined by a set of knots t1  ≤ t2  ≤  ...  ≤  tn+k such that

  • t1 = ... = tk
  • tn+1 = ... = tn+k
  • ti < ti+k for all i

    • The family includes n members indexed by i = 1,...,n.

    Properties

    An M-spline Mi(x|k, t) has the following mathematical properties

  • Mi(x|k, t) is non-negative
  • Mi(x|k, t) is zero unless ti ≤ x < ti+k
  • Mi(x|k, t) has k − 2 continuous derivatives at interior knots tk+1, ..., tn−1
  • Mi(x|k, t) integrates to 1

    • Computation

    M-splines can be efficiently and stably computed using the following recursions:

    For k = 1,

    M i ( x | 1 , t ) = 1 t i + 1 − t i

    if ti ≤ x < ti+1, and Mi(x|1,t) = 0 otherwise.

    For k > 1,

    M i ( x | k , t ) = k [ ( x − t i ) M i ( x | k − 1 , t ) + ( t i + k − x ) M i + 1 ( x | k − 1 , t ) ] ( k − 1 ) ( t i + k − t i ) .

    Applications

    M-splines can be integrated to produce a family of monotone splines called I-splines. M-splines can also be used directly as basis splines for regression analysis involving positive response data (constraining the regression coefficients to be non-negative).

    References

    M-spline Wikipedia
    (Text) CC BY-SA