Longest common substring problem

Example

The longest common substring of the strings "ABABC", "BABCA" and "ABCBA" is string "ABC" of length 3. Other common substrings are "A", "AB", "B", "BA", "BC" and "C".

ABABC ||| BABCA ||| ABCBA

Problem definition

Given two strings, S of length m and T of length n , find the longest strings which are substrings of both S and T .

A generalization is the k-common substring problem. Given the set of strings S = { S 1 , . . . , S K } , where | S i | = n i and Σ n i = N . Find for each 2 ≤ k ≤ K , the longest strings which occur as substrings of at least k strings.

Algorithms

One can find the lengths and starting positions of the longest common substrings of S and T in Θ ( n + m ) time with the help of a generalized suffix tree. Finding them by dynamic programming costs Θ ( n m ) . The solutions to the generalized problem take Θ ( n 1 + . . . + n K ) space and Θ ( n 1 ·...· n K ) time with dynamic programming and take Θ ( N ∗ K ) time with generalized suffix tree.

Suffix tree

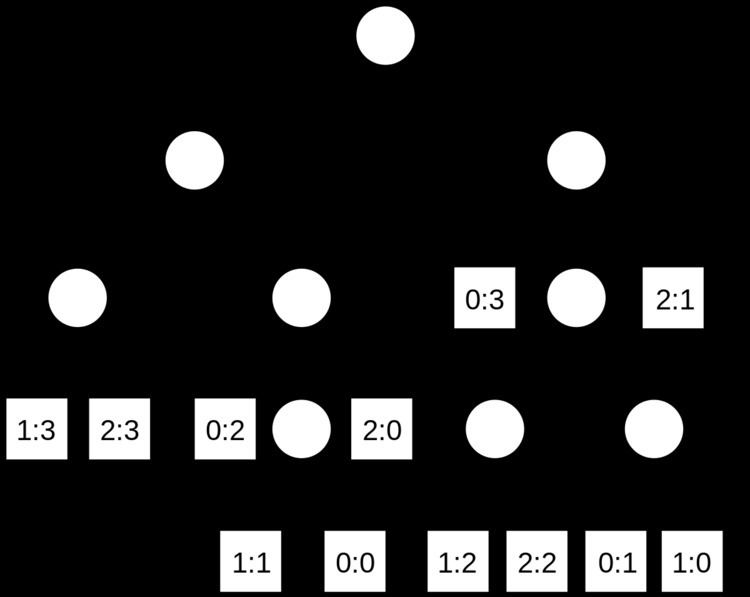
The longest common substrings of a set of strings can be found by building a generalized suffix tree for the strings, and then finding the deepest internal nodes which have leaf nodes from all the strings in the subtree below it. The figure on the right is the suffix tree for the strings "ABAB", "BABA" and "ABBA", padded with unique string terminators, to become "ABAB$0", "BABA$1" and "ABBA$2". The nodes representing "A", "B", "AB" and "BA" all have descendant leaves from all of the strings, numbered 0, 1 and 2.

Building the suffix tree takes Θ ( N ) time (if the size of the alphabet is constant). If the tree is traversed from the bottom up with a bit vector telling which strings are seen below each node, the k-common substring problem can be solved in Θ ( N K ) time. If the suffix tree is prepared for constant time lowest common ancestor retrieval, it can be solved in Θ ( N ) time.

Dynamic programming

First find the longest common suffix for all pairs of prefixes of the strings. The longest common suffix is

L C S u f f ( S 1.. p , T 1.. q ) = { L C S u f f ( S 1.. p − 1 , T 1.. q − 1 ) + 1 i f S [ p ] = T [ q ] 0 o t h e r w i s e .

For the example strings "ABAB" and "BABA":

The maximal of these longest common suffixes of possible prefixes must be the longest common substrings of S and T. These are shown on diagonals, in red, in the table. For this example, the longest common substrings are "BAB" and "ABA".

L C S u b s t r ( S , T ) = max 1 ≤ i ≤ m , 1 ≤ j ≤ n L C S u f f ( S 1.. i , T 1.. j )

This can be extended to more than two strings by adding more dimensions to the table.

Pseudocode

The following pseudocode finds the set of longest common substrings between two strings with dynamic programming:

function LCSubstr(S[1..m], T[1..n]) L := array(1..m, 1..n) z := 0 ret := {} for i := 1..m for j := 1..n if S[i] == T[j] if i == 1 or j == 1 L[i,j] := 1 else L[i,j] := L[i-1,j-1] + 1 if L[i,j] > z z := L[i,j] ret := {S[i-z+1..i]} else if L[i,j] == z ret := ret ∪ {S[i-z+1..i]} else L[i,j] := 0 return ret

This algorithm runs in O ( n m ) time. The variable z is used to hold the length of the longest common substring found so far. The set ret is used to hold the set of strings which are of length z. The set ret can be saved efficiently by just storing the index i, which is the last character of the longest common substring (of size z) instead of S[i-z+1..i]. Thus all the longest common substrings would be, for each i in ret, S[(ret[i]-z)..(ret[i])].

The following tricks can be used to reduce the memory usage of an implementation:

Keep only the last and current row of the DP table to save memory ( O ( min ( m , n ) ) instead of O ( n m ) )

Store only non-zero values in the rows. This can be done using hash tables instead of arrays. This is useful for large alphabets.