 | ||
There are many relationships among the uniform polyhedra. The Wythoff construction is able to construct almost all of the uniform polyhedra from the Schwarz triangles. The numbers that can be used for the sides of a non-dihedral Schwarz triangle that does not necessarily lead to only degenerate uniform polyhedra are 2, 3, 3/2, 4, 4/3, 5, 5/2, 5/3, and 5/4 (but numbers with numerator 4 and those with numerator 5 may not occur together). (4/2 can also be used, but only leads to degenerate uniform polyhedra as 4 and 2 have a common factor.) There are 44 such Schwarz triangles (5 with tetrahedral symmetry, 7 with octahedral symmetry and 32 with icosahedral symmetry), which, together with the infinite family of dihedral Schwarz triangles, can form almost all of the non-degenerate uniform polyhedra. Many degenerate uniform polyhedra, with completely coincident vertices, edges, or faces, may also be generated by the Wythoff construction, and those that arise from Schwarz triangles not using 4/2 are also given in the tables below along with their non-degenerate counterparts.
Contents
- Mbius and Schwarz triangles
- Summary table
- Dihedral prismatic
- Tetrahedral
- Octahedral
- Icosahedral
- Hemi forms
- Reduced forms
- Other forms
- References
There are a few non-Wythoffian uniform polyhedra, which no Schwarz triangles can generate; however, most of them can be generated using the Wythoff construction as double covers (the non-Wythoffian polyhedron is covered twice instead of once) or with several additional faces (see Omnitruncated polyhedron#Other even-sided nonconvex polyhedra). Such polyhedra are marked by an asterisk in this list. The only uniform polyhedra which still fail to be generated by the Wythoff construction are the great dirhombicosidodecahedron and the great disnub dirhombidodecahedron.
Each tiling of Schwarz triangles on a sphere may cover the sphere only once, or it may instead wind round the sphere a whole number of times, crossing itself in the process. The number of times the tiling winds round the sphere is the density of the tiling, and is denoted μ.
Jonathan Bowers' short names for the polyhedra, known as Bowers acronyms, are used instead of the full names for the polyhedra to save space. The Maeder index is also given. Except for the dihedral Schwarz triangles, the Schwarz triangles are ordered by their densities.
Möbius and Schwarz triangles
According to (Coxeter, "Uniform polyhedra", 1954), there are 4 spherical triangles with angles π/p, π/q, π/r, where (p q r) are integers:
- (2 2 r) - Dihedral
- (2 3 3) - Tetrahedral
- (2 3 4) - Octahedral
- (2 3 5) - Icosahedral
These are called Möbius triangles.
In addition Schwarz triangles consider (p q r) which are rational numbers. Each of these can be classified in one of the 4 sets above.
Summary table
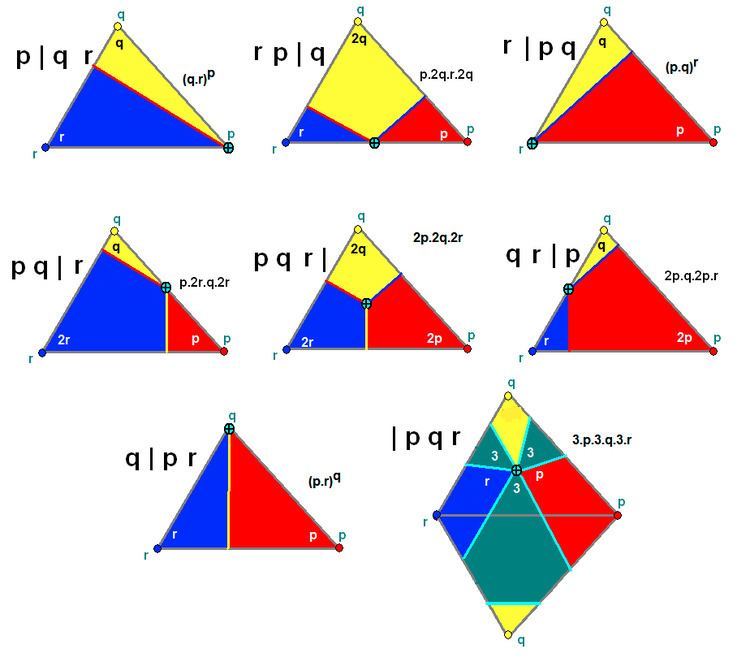
There are seven generator points with each set of p,q,r (and a few special forms):
There are four special cases:
s | – This is a mixture of p q r | and p q s |. Both the symbols p q r | and p q s | generate a common base polyhedron with some extra faces. The notation p q r
s | then represents the base polyhedron, made up of the faces common to both p q r | and p q s |.
This conversion table from Wythoff symbol to vertex configuration fails in a few exceptional uniform polyhedra. The only non-degenerate such cases are the great truncated cuboctahedron (2 3 4/3 |), truncated dodecadodecahedron (2 5/3 5 |), great icosahedron (| 2 3/2 3/2), great retrosnub icosidodecahedron (| 2 3/2 5/3), and the small snub icosicosidodecahedron (| 3/2 3/2 5/2). In these cases the vertex figure is highly distorted to achieve uniformity with flat faces: in the first two cases it is an obtuse triangle instead of an acute triangle, and in the last three it is a pentagram or hexagram instead of a pentagon or hexagon, winding around the centre twice. This results in some faces being pushed right through the polyhedron when compared with the topologically equivalent forms without the vertex figure distortion and coming out retrograde on the other side. For the same reason, the densities of these polyhedra are not the same as the density of the Schwarz triangles that give rise to them, being instead 1, 3, 7, 37, and 38 respectively.
Dihedral (prismatic)
In dihedral Schwarz triangles, two of the numbers are 2, and the third may be any rational number strictly greater than 1.
- (2 2 n/d) – degenerate if gcd(n, d) > 1.
Many of the polyhedra with dihedral symmetry have digon faces that make them degenerate polyhedra (e.g. dihedra and hosohedra). Columns of the table that only give degenerate uniform polyhedra are not included: special degenerate cases (only in the (2 2 2) Schwarz triangle) are marked with a large cross. Crossed antiprisms with a base {p} where p < 3/2 cannot exist as their vertex figures would violate the triangular inequality; these are also marked with a large cross. The 3/2-crossed antiprism (trirp) is degenerate, being flat in Euclidean space, and is also marked with a large cross. The Schwarz triangles (2 2 n/d) are listed here only when gcd(n, d) = 1, as they otherwise result in only degenerate uniform polyhedra.
The list below gives all possible cases where n ≤ 6.
Tetrahedral
In tetrahedral Schwarz triangles, the maximum numerator allowed is 3.
Octahedral
In octahedral Schwarz triangles, the maximum numerator allowed is 4. There also exist octahedral Schwarz triangles which use 4/2 as a number, but these only lead to degenerate uniform polyhedra as 4 and 2 have a common factor.
Icosahedral
In icosahedral Schwarz triangles, the maximum numerator allowed is 5. Additionally, the numerator 4 cannot be used at all in icosahedral Schwarz triangles, although numerators 2 and 3 are allowed. (If 4 and 5 could occur together in some Schwarz triangle, they would have to do so in some Möbius triangle as well; but this is impossible as (2 4 5) is a hyperbolic triangle, not a spherical one.)
Hemi forms
These polyhedra (the hemipolyhedra) are generated as double coverings by the Wythoff construction. If a figure generated by the Wythoff construction is composed of two identical components, the "hemi" operator takes only one.
Reduced forms
These polyhedra are generated with extra faces by the Wythoff construction. If a figure is generated by the Wythoff construction as being composed of two or three non-identical components, the "reduced" operator removes extra faces (that must be specified) from the figure, leaving only one component.
The tetrahemihexahedron (thah, U4) is also a reduced version of the {3/2}-cupola (retrograde triangular cupola, ratricu) by {6/2}. As such it may also be called the crossed triangular cuploid.
Other forms
These two uniform polyhedra cannot be generated at all by the Wythoff construction. This is the set of uniform polyhedra commonly described as the "non-Wythoffians". Instead of the triangular fundamental domains of the Wythoffian uniform polyhedra, these two polyhedra have tetragonal fundamental domains.
Skilling's figure is not given an index in Maeder's list due to it being an exotic uniform polyhedron, with ridges (edges in the 3D case) completely coincident. This is also true of some of the degenerate polyhedron included in the above list, such as the small complex icosidodecahedron. This interpretation of edges being coincident allows these figures to have two faces per edge: not doubling the edges would give them 4, 6, 8, 10 or 12 faces meeting at an edge, figures that are usually excluded as uniform polyhedra. Skilling's figure has 4 faces meeting at some edges.
