Samiksha Jaiswal (Editor)

Liouville function

Updated on
Edit
Like
Comment
Share on FacebookTweet on TwitterShare on LinkedInShare on Reddit
Liouville function

The Liouville function, denoted by λ(n) and named after Joseph Liouville, is an important function in number theory.

Contents

If n is a positive integer, then λ(n) is defined as:

λ ( n ) = ( − 1 ) Ω ( n ) ,

where Ω(n) is the number of prime factors of n, counted with multiplicity (sequence A008836 in the OEIS).

λ is completely multiplicative since Ω(n) is completely additive, i.e.: Ω(ab) = Ω(a) + Ω(b). The number 1 has no prime factors, so Ω(1) = 0 and therefore λ(1) = 1. The Liouville function satisfies the identity:

∑ d | n λ ( d ) = { 1 if  n  is a perfect square, 0 otherwise.

The Liouville function's Dirichlet inverse is the absolute value of the Möbius function.

Series

The Dirichlet series for the Liouville function is related to the Riemann zeta function by

ζ ( 2 s ) ζ ( s ) = ∑ n = 1 ∞ λ ( n ) n s .

The Lambert series for the Liouville function is

∑ n = 1 ∞ λ ( n ) q n 1 − q n = ∑ n = 1 ∞ q n 2 = 1 2 ( ϑ 3 ( q ) − 1 ) ,

where ϑ 3 ( q ) is the Jacobi theta function.

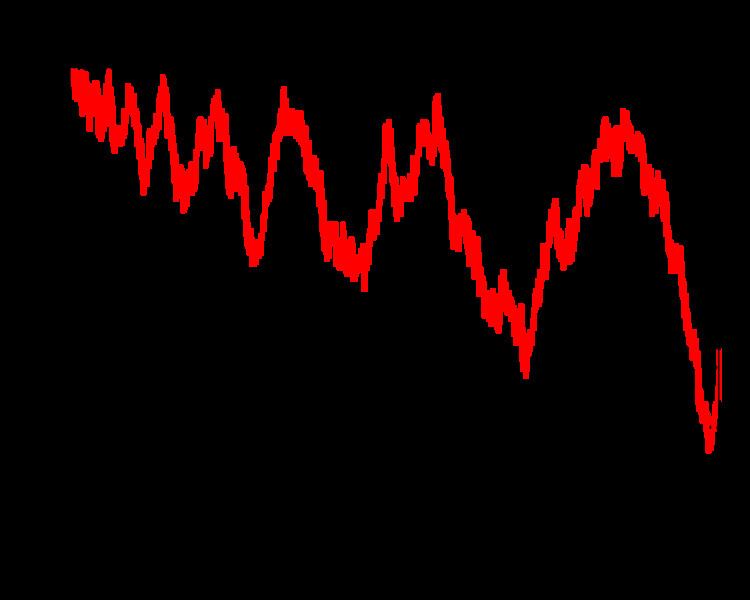
Conjectures

The Pólya conjecture is a conjecture made by George Pólya in 1919. Defining

L ( n ) = ∑ k = 1 n λ ( k ) ,

the conjecture states that L ( n ) ≤ 0 for n > 1. This turned out to be false. The smallest counter-example is n = 906150257, found by Minoru Tanaka in 1980. It has since been shown that L(n) > 0.0618672√n for infinitely many positive integers n, while it can also be shown via the same methods that L(n) < -1.3892783√n for infinitely many positive integers n.

Define the related sum

T ( n ) = ∑ k = 1 n λ ( k ) k .

It was open for some time whether T(n) ≥ 0 for sufficiently big n ≥ n0 (this conjecture is occasionally–though incorrectly–attributed to Pál Turán). This was then disproved by Haselgrove (1958), who showed that T(n) takes negative values infinitely often. A confirmation of this positivity conjecture would have led to a proof of the Riemann hypothesis, as was shown by Pál Turán.

References

Liouville function Wikipedia
(Text) CC BY-SA