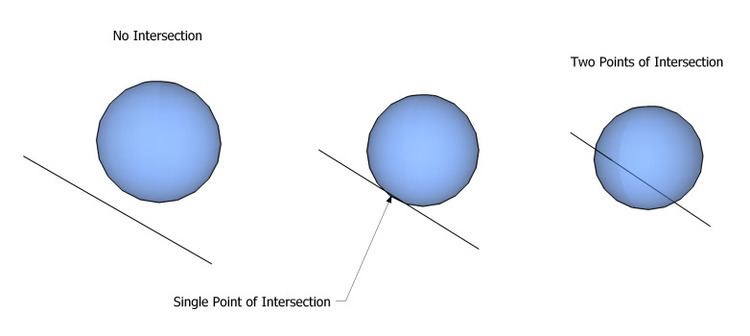
In analytic geometry, a line and a sphere can intersect in three ways: no intersection at all, at exactly one point, or in two points. Methods for distinguishing these cases, and determining equations for the points in the latter cases, are useful in a number of circumstances. For example, this is a common calculation to perform during ray tracing (Eberly 2006:698).
In vector notation, the equations are as follows:
Equation for a sphere
∥ x − c ∥ 2 = r 2 c - center point r - radius x - points on the sphereEquation for a line starting at o
x = o + d l d - distance along line from starting point l - direction of line (a unit vector) o - origin of the line x - points on the lineSearching for points that are on the line and on the sphere means combining the equations and solving for d :
Equations combinedExpandedRearrangedThe form of a
quadratic formula is now observable. (This quadratic equation is an example of Joachimsthal's Equation [1].)where
a = l ⋅ l = ∥ l ∥ 2 b = 2 ( l ⋅ ( o − c ) ) c = ( o − c ) ⋅ ( o − c ) − r 2 = ∥ o − c ∥ 2 − r 2 SimplifiedNote that
l is a unit vector, and thus
∥ l ∥ 2 = 1 . Thus, we can simplify this further to
d = − ( l ⋅ ( o − c ) ) ± ( l ⋅ ( o − c ) ) 2 − ∥ o − c ∥ 2 + r 2 If the value under the square-root ( ( l ⋅ ( o − c ) ) 2 − ∥ o − c ∥ 2 + r 2 ) is less than zero, then it is clear that no solutions exist, i.e. the line does not intersect the sphere (case 1).If it is zero, then exactly one solution exists, i.e. the line just touches the sphere in one point (case 2).If it is greater than zero, two solutions exist, and thus the line touches the sphere in two points (case 3).