Lifting line theory

Introduction

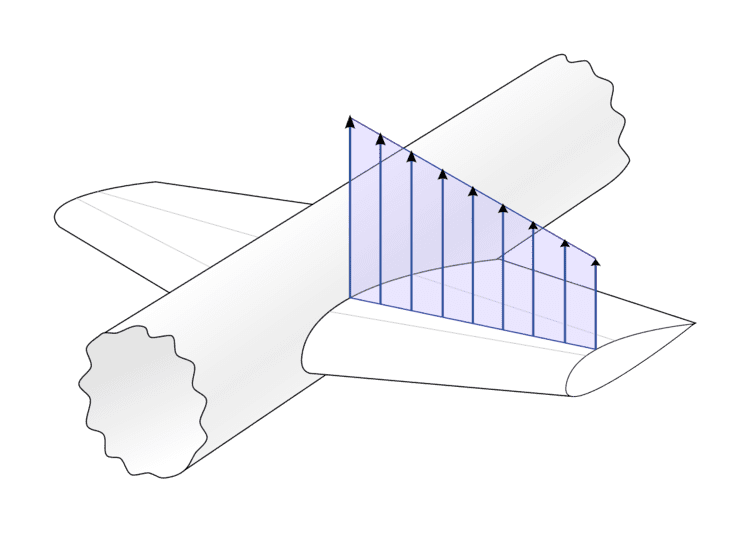
On a three-dimensional, finite wing, lift over each wing segment (local lift per unit span, l or L ~ ) does not correspond simply to what two-dimensional analysis predicts. Instead, this local amount of lift is strongly affected by the lift generated at neighboring wing sections.

As such, it is difficult to predict analytically the overall amount of lift that a wing of given geometry will generate. The lifting-line theory yields the lift distribution along the span-wise direction, L ~ ( y ) based only on the wing geometry (span-wise distribution of chord, airfoil, and twist) and flow conditions ( ρ , V ∞ , α ∞ ).

Principle

The lifting-line theory applies the concept of circulation and the Kutta–Joukowski theorem,

so that instead of the lift distribution function, the unknown effectively becomes the distribution of circulation over the span, Γ ( y ) .

Modeling the (unknown and sought-after) local lift with the (also unknown) local circulation allows us to account for the influence of one section over its neighbors. In this view, any span-wise change in lift is equivalent to a span-wise change of circulation. According to the Helmholtz theorems, a vortex filament cannot begin or terminate in the air. As such, any span-wise change in lift can be modeled as the shedding of a vortex filament down the flow, behind the wing.

This shed vortex, whose strength is the derivative of the (unknown) local wing circulation distribution, d ⁡ Γ d ⁡ y , influences the flow left and right of the wing section.

This sideways influence (upwash on the outboard, downwash on the inboard) is the key to the lifting-line theory. Now, if the change in lift distribution is known at given lift section, it is possible to predict how that section influences the lift over its neighbors: the vertical induced velocity (upwash or downwash, ω i ) can be quantified using the velocity distribution within a vortex, and related to a change in effective angle of attack over neighboring sections.

In mathematical terms, the local induced change of angle of attack α i on a given section can be quantified with the integral sum of the downwash induced by every other wing section. In turn, the integral sum of the lift on each downwashed wing section is equal to the (known) total desired amount of lift.

This leads to an integro-differential equation in the form of L t o t a l = ρ V ∞ ∫ t i p t i p Γ ( y ) d ⁡ y where Γ ( y ) is expressed solely in terms of the wing geometry and its own span-wise variation, d ⁡ Γ ( y ) d ⁡ y . The solution to this equation is a function, Γ ( y ) , that accurately describes the circulation (and therefore lift) distribution over a finite wing of known geometry.

Derivation

(Based on.)

Nomenclature:

The following are all functions of the wings span-wise station y (i.e. they can all vary along the wing)

To derive the model we start with the assumption that the circulation of the wing varies as a function of the spanwise locations. The function assumed is a Fourier function. Firstly, the coordinate for the spanwise location y is transformed by y = s c o s θ , where y is spanwise location, and s is the semi-span of the wing.

and so the circulation is assumed to be:

Γ ( y ) = Γ ( θ ) = γ = 4 s V ∞ ∑ n A n sin ⁡ ( n θ ) ( 1 )

Since the circulation of a section is related the C l by the equation:

C l = 2 γ V ∞ c ( 2 )

but since the coefficient of lift is a function of angle of attack:

C l = C l α ( α ∞ + α g e o − α 0 − α i ) ( 3 )

hence the vortex strength at any particular spanwise station can be given by the equations:

γ = 1 2 V ∞ c C l α ( α ∞ + α g e o − α 0 − α i ) ( 4 )

This one equation has two unknowns: the value for γ and the value for α i . However, the downwash is purely a function of the circulation only. So we can determine the value α i in terms of Γ ( y ) , bring this term across to the left hand side of the equation and solve. The downwash at any given station is a function of the entire shed vortex system. This is determined by integrating the influence of each differential shed vortex over the span of the wing.

Differential element of circulation:

d Γ = 4 s V ∞ ∑ n = 1 ∞ n A n cos ⁡ ( n θ ) ( 5 )

Differential downwash due to the differential element of circulation (acts like half an infinite vortex line):

d w i = d Γ 4 π r ( 6 )

The integral equation over the span of the wing to determine the downwash at a particular location is:

w i = ∫ − s s 1 y − y 0 d Γ ( 7 )

After appropriate substitutions and integrations we get:

w i = V ∞ ∑ n = 1 ∞ n A n sin ⁡ ( n θ ) sin ⁡ ( θ ) ( 8 )

And so the change in angle attack is determined by (assuming small angles):

α i = w i V ∞ ( 9 )

By substituting equations 8 and 9 into RHS of equation 4 and equation 1 into the LHS of equation 4, we then get:

4 s V ∞ ∑ n = 1 ∞ A n sin ⁡ ( n θ ) = 1 2 V ∞ c C l α [ α ∞ + α g e o − α 0 − ∑ n = 1 ∞ n A n sin ⁡ ( n θ ) sin ⁡ ( θ ) ] ( 10 )

After rearranging, we get the series of simultaneous equations:

∑ n = 1 ∞ A n sin ⁡ ( n θ ) ( sin ⁡ ( θ ) + n C l α c 8 s ) = C l α c 8 s sin ⁡ ( θ ) ( α ∞ + α g e o − α 0 ) ( 11 )

By taking a finite number of terms, equation 11 can be expressed in matrix form and solved for coefficients A. Note the left-hand side of the equation represents each element in the matrix, and the terms on the RHS of equation 11 represent the RHS of the matrix form. Each row in the matrix form represents a different span-wise station, and each column represents a different value for n.

Appropriate choices for θ are as a linear variation between ( − π , π ) . Note that this range does not include the values for π , as this leads to a singular matrix, which can't be solved.

Lift and drag from coefficients

The lift can be determined by integrating the circulation terms:

Lift = ρ V ∞ ∫ − s s Γ d y

which can be reduced to:

C L = π A R A 1

where A 1 is the first term of the solution of the simultaneous equations shown above.

The induced drag can be determined from

Drag induced = ρ V ∞ ∫ − s s Γ sin ⁡ α i d y

or

C D induced = π A R ∑ n = 1 ∞ n A n 2 = C L 2 π A R ( 1 + ∑ n = 2 ∞ n A n 2 A 1 2 ) = C L 2 π A R e

where

δ = ∑ n = 2 ∞ n A n 2 A 1 2

e = 1 1 + δ is the span efficiency factor

Symmetric wing

For a symmetric wing, the even terms of the series coefficients are identically equal to 0, and so can be dropped.

Rolling wings

When the aircraft is rolling, an additional term can be added that adds the wing station distance multiplied by the rate of roll to give additional angle of attack change. Equation 3 then becomes:

C l = C l α ( α ∞ + α g e o − α 0 − α i + p y s ) ( 3 )

where

Note that y can be negative, which introduces non-zero even coefficients in the equation that must be accounted for.

Control deflection

The effect of ailerons can be accounted for simply changing α 0 term in Equation 3. For non-symmetric controls such as ailerons the α 0 term changes on each side of the wing.

Elliptical wings

For an elliptical wing with no twist, with:

y ( θ ) = s cos ⁡ ( θ )

The chord length is given as a function of span location as:

c ( θ ) = c r o o t sin ⁡ ( θ )

Also,

e = 1

This yields the famous equation for the elliptic induced drag coefficient:

C D i = C L 2 π A R

where

Useful approximations

A useful approximation is that

where

The theoretical value for   C l α is 2 π . Note that this equation becomes the thin airfoil equation if AR goes to infinity.

Lifting-line theory also states an equation for induced drag:.

where

Limitations of the theory

The lifting line theory does not take into account the following: