 | ||
Legendre's conjecture, proposed by Adrien-Marie Legendre, states that there is a prime number between n2 and (n + 1)2 for every positive integer n. The conjecture is one of Landau's problems (1912) on prime numbers; as of 2016, the conjecture has neither been proved nor disproved.
Contents
Prime gaps
Legendre's conjecture is one of a family of results and conjectures related to prime gaps, that is, to the spacing between prime numbers.
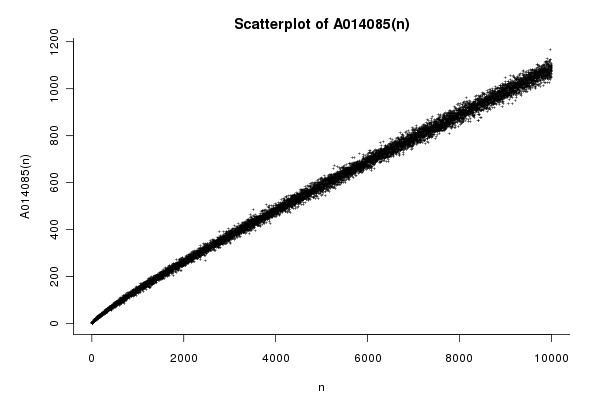
The prime number theorem implies that the actual number of primes between n2 and (n + 1)2 A014085 is asymptotic to n/ln(n). Since this number is large for large n, this lends credence to Legendre's conjecture.
If Legendre's conjecture is true, the gap between any prime p and the next largest prime would always be at most on the order of
Harald Cramér conjectured that the gaps are always much smaller, of the order
A counterexample near 1018 would require a prime gap fifty million times the size of the average gap.
Legendre's conjecture implies that at least one prime can be found in every half revolution of the Ulam spiral.
Partial results
Baker, Harman and Pintz proved that there is a prime in the interval
A table of maximal prime gaps shows that the conjecture holds to
It has been proven that for infinitely many
where
