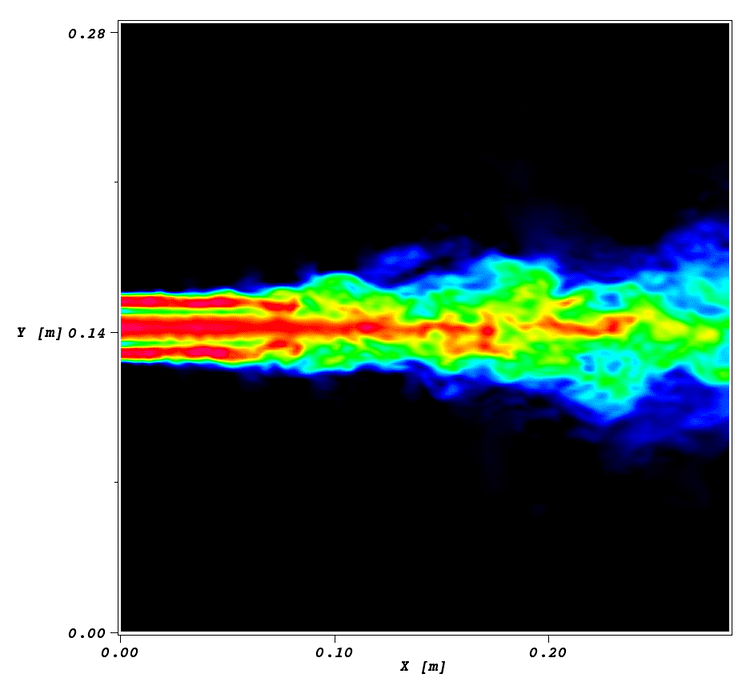
Large eddy simulation

Filter definition and properties

An LES filter can be applied to a spatial and temporal field ϕ ( x , t ) and perform a spatial filtering operation, a temporal filtering operation, or both. The filtered field, denoted with a bar, is defined as:

where G is the filter convolution kernel. This can also be written as:

The filter kernel G has an associated cutoff length scale Δ and cutoff time scale τ c . Scales smaller than these are eliminated from ϕ ¯ . Using the above filter definition, any field ϕ may be split up into a filtered and sub-filtered (denoted with a prime) portion, as

It is important to note that the large eddy simulation filtering operation does not satisfy the properties of a Reynolds operator.

Filtered governing equations

The governing equations of LES are obtained by filtering the partial differential equations governing the flow field ρ u ( x , t ) . There are differences between the incompressible and compressible LES governing equations, which lead to the definition of a new filtering operation.

Incompressible flow

For incompressible flow, the continuity equation and Navier–Stokes equations are filtered, yielding the filtered incompressible continuity equation,

and the filtered Navier–Stokes equations,

where p ¯ is the filtered pressure field and S i j is the rate-of-strain tensor. The nonlinear filtered advection term u i u j ¯ is the chief cause of difficulty in LES modeling. It requires knowledge of the unfiltered velocity field, which is unknown, so it must be modeled. The analysis that follows illustrates the difficulty caused by the nonlinearity, namely, that it causes interaction between large and small scales, preventing separation of scales.

The filtered advection term can be split up, following Leonard (1974), as:

where τ i j r is the residual stress tensor, so that the filtered Navier Stokes equations become

with the residual stress tensor τ i j r grouping all unclosed terms. Leonard decomposed this stress tensor as τ i j r = L i j + C i j + R i j and provided physical interpretations for each term. L i j , the Leonard tensor, represents interactions among large scales, R i j , the Reynolds stress-like term, represents interactions among the sub-filter scales (SFS), and C i j , the Clark tensor, represents cross-scale interactions between large and small scales. Modeling the unclosed term τ i j r is the task of SFS models (also referred to as sub-grid scale, or SGS, models). This is made challenging by the fact that the sub-filter scale stress tensor τ i j r must account for interactions among all scales, including filtered scales with unfiltered scales.

The filtered governing equation for a passive scalar ϕ , such as mixture fraction or temperature, can be written as

where J ϕ is the diffusive flux of ϕ , and q i j is the sub-filter stress tensor for the scalar ϕ . The filtered diffusive flux J ϕ ¯ is unclosed, unless a particular form is assumed for it (e.g. a gradient diffusion model J ϕ = D ϕ ∂ ϕ ∂ x i ). q i j is defined analogously to τ i j r ,

and can similarly be split up into contributions from interactions between various scales. This sub-filter tensor also requires a sub-filter model.

Derivation

Using Einstein notation, the Navier–Stokes equations for an incompressible fluid in Cartesian coordinates are

Filtering the momentum equation results in

If we assume that filtering and differentiation commute, then

This equation models the changes in time of the filtered variables u i ¯ . Since the unfiltered variables u i are not known, it is impossible to directly calculate ∂ u i u j ∂ x j ¯ . However, the quantity ∂ u i ¯ u j ¯ ∂ x j is known. A substitution is made:

Let τ i j = u i u j ¯ − u i ¯ u j ¯ . The resulting set of equations are the LES equations:

Compressible governing equations

For the governing equations of compressible flow, each equation, starting with the conservation of mass, is filtered. This gives:

which results in an additional sub-filter term. However, it is desirable to avoid having to model the sub-filter scales of the mass conservation equation. For this reason, Favre proposed a density-weighted filtering operation, called Favre filtering, defined for an arbitrary quantity ϕ as:

which, in the limit of incompressibility, becomes the normal filtering operation. This makes the conservation of mass equation:

This concept can then be extended to write the Favre-filtered momentum equation for compressible flow. Following Vreman:

where σ i j is the shear stress tensor, given for a Newtonian fluid by:

and the term ∂ ∂ x j ( σ ¯ i j − σ ~ i j ) represents a sub-filter viscous contribution from evaluating the viscosity μ ( T ) using the Favre-filtered temperature T ~ . The subgrid stress tensor for the Favre-filtered momentum field is given by

By analogy, the Leonard decomposition may also be written for the residual stress tensor for a filtered triple product ρ ϕ ψ ¯ . The triple product can be rewritten using the Favre filtering operator as ρ ¯ ϕ ψ ~ , which is an unclosed term (it requires knowledge of the fields ϕ and ψ , when only the fields ϕ ~ and ψ ~ are known). It can be broken up in a manner analogous to u i u j ¯ above, which results in a sub-filter stress tensor ρ ¯ ( ϕ ψ ~ − ϕ ~ ψ ~ ) . This sub-filter term can be split up into contributions from three types of interactions: the Leondard tensor L i j , representing interactions among resolved scales; the Clark tensor C i j , representing interactions between resolved and unresolved scales; and the Reynolds tensor R i j , which represents interactions among unresolved scales.

Filtered kinetic energy equation

In addition to the filtered mass and momentum equations, filtering the kinetic energy equation can provide additional insight. The kinetic energy field can be filtered to yield the total filtered kinetic energy:

and the total filtered kinetic energy can be decomposed into two terms: the kinetic energy of the filtered velocity field E f ,

and the residual kinetic energy k r ,

such that E ¯ = E f + k r .

The conservation equation for E f can be obtained by multiplying the filtered momentum transport equation by u i ¯ to yield:

where ϵ f = 2 ν S i j ¯ S i j ¯ is the dissipation of kinetic energy of the filtered velocity field by viscous stress, and Π = − τ i j r S i j ¯ represents the sub-filter scale (SFS) dissipation of kinetic energy.

The terms on the left-hand side represent transport, and the terms on the right-hand side are sink terms that dissipate kinetic energy.

The Π SFS dissipation term is of particular interest, since it represents the transfer of energy from large resolved scales to small unresolved scales. On average, Π transfers energy from large to small scales. However, instantaneously Π can be positive or negative, meaning it can also act as a source term for E f , the kinetic energy of the filtered velocity field. The transfer of energy from unresolved to resolved scales is called backscatter (and likewise the transfer of energy from resolved to unresolved scales is called forward-scatter).

Numerical methods for LES

Large eddy simulation involves the solution to the discrete filtered governing equations using computational fluid dynamics. LES resolves scales from the domain size L down to the filter size Δ , and as such a substantial portion of high wave number turbulent fluctuations must be resolved. This requires either high-order numerical schemes, or fine grid resolution if low-order numerical schemes are used. Chapter 13 of Pope addresses the question of how fine a grid resolution Δ x is needed to resolve a filtered velocity field u ¯ ( x ) . Ghosal found that for low-order discretization schemes, such as those used in finite volume methods, the truncation error can be the same order as the subfilter scale contributions, unless the filter width Δ is considerably larger than the grid spacing Δ x . While even-order schemes have truncation error, they are non-dissipative, and because subfilter scale models are dissipative, even-order schemes will not affect the subfilter scale model contributions as strongly as dissipative schemes.

Filter implementation

The filtering operation in large eddy simulation can be implicit or explicit. Implicit filtering recognizes that the subfilter scale model will dissipate in the same manner as many numerical schemes. In this way, the grid, or the numerical discretization scheme, can be assumed to be the LES low-pass filter. While this takes full advantage of the grid resolution, and eliminates the computational cost of calculating a subfilter scale model term, it is difficult to determine the shape of the LES filter that is associated with some numerical issues. Additionally, truncation error can also become an issue.

In explicit filtering, an LES filter is applied to the discretized Navier–Stokes equations, providing a well-defined filter shape and reducing the truncation error. However, explicit filtering requires a finer grid than implicit filtering, and the computational cost increases with ( Δ x ) 4 . Chapter 8 of Sagaut (2006) covers LES numerics in greater detail.

Modeling unresolved scales

To discuss the modeling of unresolved scales, first the unresolved scales must be classified. They fall into two groups: resolved sub-filter scales (SFS), and sub-grid scales(SGS).

The resolved sub-filter scales represent the scales with wave numbers larger than the cutoff wave number k c , but whose effects are dampened by the filter. Resolved sub-filter scales only exist when filters non-local in wave-space are used (such as a box or Gaussian filter). These resolved sub-filter scales must be modeled using filter reconstruction.

Sub-grid scales are any scales that are smaller than the cutoff filter width Δ . The form of the SGS model depends on the filter implementation. As mentioned in the Numerical methods for LES section, if implicit LES is considered, no SGS model is implemented and the numerical effects of the discretization are assumed to mimic the physics of the unresolved turbulent motions.

Sub-grid scale models

Without a universally valid description of turbulence, empirical information must be utilized when constructing and applying SGS models, supplemented with fundamental physical constraints such as Galilean invariance . Two classes of SGS models exist; the first class is functional models and the second class is structural models. Some models may be categorized as both.

Functional (eddy–viscosity) models

Functional models are simpler than structural models, focusing only on dissipating energy at a rate that is physically correct. These are based on an artificial eddy viscosity approach, where the effects of turbulence are lumped into a turbulent viscosity. The approach treats dissipation of kinetic energy at sub-grid scales as analogous to molecular diffusion. In this case, the deviatoric part of τ i j is modeled as:

where ν t is the turbulent eddy viscosity and S ¯ i j = 1 2 ( ∂ u ¯ i ∂ x j + ∂ u ¯ j ∂ x i ) is the rate-of-strain tensor.

Based on dimensional analysis, the eddy viscosity must have units of [ ν t ] = m 2 s . Most eddy viscosity SGS models model the eddy viscosity as the product of a characteristic length scale and a characteristic velocity scale.

Smagorinsky–Lilly model

The first SGS model developed was the Smagorinsky–Lilly SGS model, which was developed by Smagorinsky and used in the first LES simulation by Deardorff. It models the eddy viscosity as:

where Δ g is the grid size and C s is a constant.

This method assumes that the energy production and dissipation of the small scales are in equilibrium - that is, ϵ = Π .

Germano dynamic model

Germano et al. identified a number of studies using the Smagorinsky model that each found different values for the Smagorinsky constant C s for different flow configurations. In an attempt to formulate a more universal approach to SGS models, Germano et al. proposed a dynamic Smagorinsky model, which utilized two filters: a grid LES filter, denoted ⋅ ¯ , and a test LES filter, denoted ⋅ ^ . In this case, the resolved turbulent stress tensor L i j is defined as

which is also called the Germano identity. The quantity T i j r = u i u j ¯ ^ − u ¯ ^ i u ¯ ^ j is the residual stress tensor for the test filter scale, and τ ^ i j r = u i u j ¯ ^ − u ¯ i u ¯ j ^ is the residual stress tensor for the grid filter, then test filtered.

L i j represents the contribution to the SGS stresses by length scales smaller than the test filter width Δ ^ but larger than the grid filter width Δ ¯ . The dynamic model then finds the coefficient that best complies with the Germano identity. However, since the identity is a tensorial equation, it is overdetermined (five equations for one unknown), prompting Lilly to propose a minimum least-square error method that leads to an equation for C s :

where

However, this procedure was numerically unstable since the numerator could become negative and large fluctuations in C s were often observed. Hence, additional averaging of the error in the minimization is often employed, leading to:

This has made the dynamic model more stable and making the method more widely applicable. Inherent in the procedure is the assumption that the coefficient C s is invariant of scale (see review ). The averaging can be a spatial averaging over directions of statistical homogeneity (e.g. volume for homogeneous turbulence or wall-parallel planes for channel flow as originally used in Germano et al.), or time following Lagrangian fluid trajectories .