 | ||
High-resolution schemes are used in the numerical solution of partial differential equations where high accuracy is required in the presence of shocks or discontinuities. They have the following properties:
General methods are often not adequate for accurate resolution of steep gradient phenomena; they usually introduce non-physical effects such as smearing of the solution or spurious oscillations. Since publication of Godunov's order barrier theorem, which proved that linear methods cannot provide non-oscillatory solutions higher than first order (Godunov-1954, Godunov-1959), these difficulties have attracted a lot of attention and a number of techniques have been developed that largely overcome these problems. To avoid spurious or non-physical oscillations where shocks are present, schemes that exhibit a Total Variation Diminishing (TVD) characteristic are especially attractive.
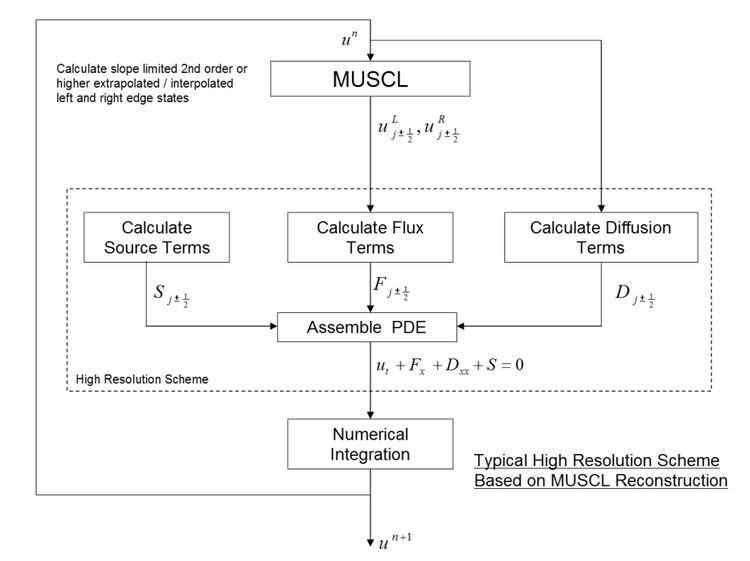
Two techniques that are proving to be particularly effective are MUSCL (Monotone Upstream-Centered Schemes for Conservation Laws) a flux/slope limiter method (van Leer-1979, Hirsch-1990, Tannehill-1997, Laney-1998, Toro-1999) and the WENO (Weighted Essentially Non-Oscillatory) method (Shu-1998, Shu-2009). Both methods are usually referred to as high resolution schemes (see diagram).
MUSCL methods are generally second-order accurate in smooth regions (although they can be formulated for higher orders) and provide good resolution, monotonic solutions around discontinuities. They are straight-forward to implement and are computationally efficient.
For problems comprising both shocks and complex smooth solution structure, WENO schemes can provide higher accuracy than second-order schemes along with good resolution around discontinuities. Most applications tend to use a fifth order accurate WENO scheme, whilst higher order schemes can be used where the problem demands improved accuracy in smooth regions.
