 | ||
In mathematics, the Lambert-W function, also called the omega function or product logarithm, is a set of functions, namely the branches of the inverse relation of the function f(z) = zez where ez is the exponential function and z is any complex number. In other words
Contents
- Terminology
- History
- Derivative
- Antiderivative
- Asymptotic expansions
- Integer and complex powers
- Identities
- Special values
- Definite integrals
- Indefinite integrals
- Applications
- Example 1
- Example 2
- Example 3
- Example 4
- Example 5
- Example 6
- Example 7
- Example 8
- Example 9
- Example 10
- Example 11
- Example 12
- Example 13
- Example 14
- Example 15
- Example 16
- Generalizations
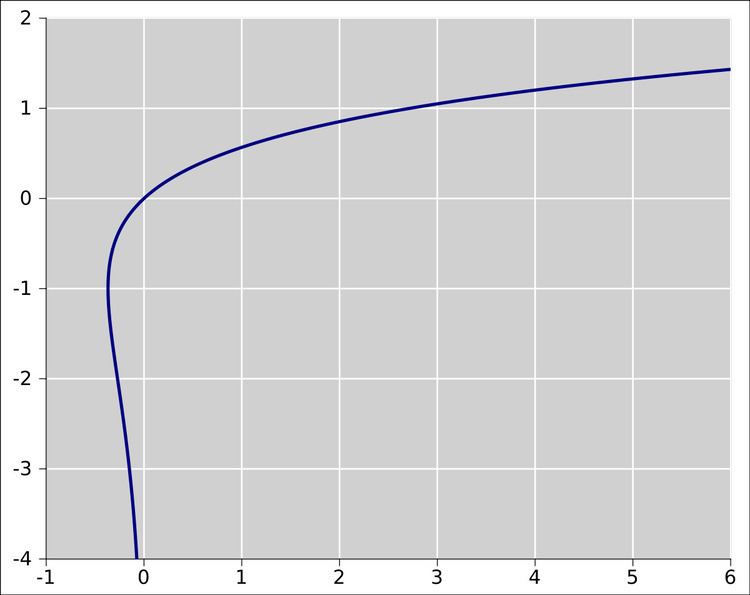
- Plots
- Numerical evaluation
- Software
- References
By substituting the above equation in
for any complex number z'.
Since the function ƒ is not injective, the relation W is multivalued (except at 0). If we restrict attention to real-valued W, the complex variable z is then replaced by the real variable x, and the relation is defined only for x ≥ −1/e, and is double-valued on (−1/e, 0). The additional constraint W ≥ −1 defines a single-valued function W0(x). We have W0(0) = 0 and W0(−1/e) = −1. Meanwhile, the lower branch has W ≤ −1 and is denoted W−1(x). It decreases from W−1(−1/e) = −1 to W−1(0−) = −∞.
The Lambert W relation cannot be expressed in terms of elementary functions. It is useful in combinatorics, for instance in the enumeration of trees. It can be used to solve various equations involving exponentials (e.g. the maxima of the Planck, Bose–Einstein, and Fermi–Dirac distributions) and also occurs in the solution of delay differential equations, such as y'(t) = a y(t − 1). In biochemistry, and in particular enzyme kinetics, a closed-form solution for the time course kinetics analysis of Michaelis–Menten kinetics is described in terms of the Lambert W function.
Terminology
The Lambert-W function is named after Johann Heinrich Lambert. The main branch W0 is denoted by Wp in the Digital Library of Mathematical Functions and the branch W−1 is denoted by Wm there.
The notation convention chosen here (with W0 and W−1) follows the canonical reference on the Lambert-W function by Corless, Gonnet, Hare, Jeffrey and Knuth.
History
Lambert first considered the related Lambert's Transcendental Equation in 1758, which led to a paper by Leonhard Euler in 1783 that discussed the special case of wew.
The Lambert W function was "re-discovered" every decade or so in specialized applications. In 1993, when it was reported that the Lambert W function provides an exact solution to the quantum-mechanical double-well Dirac delta function model for equal charges—a fundamental problem in physics—Corless and developers of the Maple Computer algebra system made a library search, and found that this function was ubiquitous in nature.
Derivative
By implicit differentiation, one can show that all branches of W satisfy the differential equation
(W is not differentiable for z = −1/e.) As a consequence, we get the following formula for the derivative of W:
Using the identity
Antiderivative
The function W(x), and many expressions involving W(x), can be integrated using the substitution w = W(x), i.e. x = w ew:
(The last equation is more common in the literature but does not hold at
One consequence of which (using the fact that
Asymptotic expansions
The Taylor series of
The radius of convergence is 1/e, as may be seen by the ratio test. The function defined by this series can be extended to a holomorphic function defined on all complex numbers with a branch cut along the interval (−∞, −1/e]; this holomorphic function defines the principal branch of the Lambert W function.
For large values of x, W0 is asymptotic to
where
The other real branch,
In it is shown that the following bound holds for
In it was proven that branch
for
Integer and complex powers
Integer powers of
More generally, for
which is, in general, a Laurent series of order r. Equivalently, the latter can be written in the form of a Taylor expansion of powers of
which holds for any
Identities
A few identities follow from definition:
Note that, since f(x) = x⋅ex is not injective, not always W(f(x)) = x. For fixed x < 0 and x ≠ -1 the equation x⋅ex = y⋅ey has two solutions in y, one of which is of course y = x. Then, for i = 0 and x < −1 as well as for i = −1 and x ∈ (−1, 0), Wi(x⋅ex) is the other solution of the equation x⋅ex = y⋅ey.
(which can be extended to other n and x if the right branch is chosen)
From inverting f(ln(x)):
With Euler's iterated exponential h(x):
Special values
For any non-zero algebraic number x, W(x) is a transcendental number. Indeed, if W(x) is zero then x must be zero as well, and if W(x) is non-zero and algebraic, then by the Lindemann–Weierstrass theorem, eW(x) must be transcendental, implying that x=W(x)eW(x) must also be transcendental.
Definite integrals
There are several useful definite integral formulas involving the W function, including the following:
The first identity can be found by writing the Gaussian integral in polar coordinates.
The second identity can be derived by making the substitution
which gives
Thus
The third identity may be derived from the second by making the substitution
Except for z along the branch cut
where the two integral expressions are equivalent due to the symmetry of the integrand.
Indefinite integrals
Applications
Many equations involving exponentials can be solved using the W function. The general strategy is to move all instances of the unknown to one side of the equation and make it look like Y = XeX at which point the W function provides the value of the variable in X.
In other words :
Example 1
More generally, the equation
where
can be transformed via the substitution
into
giving
which yields the final solution
Example 2
or, equivalently,
since
by definition.
Example 3
taking the n-th root
let :
Example 4
Whenever the complex infinite exponential tetration
converges, the Lambert W function provides the actual limit value as
where ln(z) denotes the principal branch of the complex log function. This can be shown by observing that
if c exists, so
which is the result which was to be found.
Example 5
Solutions for
have the form
Example 6
The solution for the current in a series diode/resistor circuit can also be written in terms of the Lambert W. See diode modeling.
Example 7
The delay differential equation
has characteristic equation
Example 8
The Lambert-W function has been recently (2013) shown to be the optimal solution for the required magnetic field of a Zeeman slower.
Example 9
Granular and debris flow fronts and deposits, and the fronts of viscous fluids in natural events and in the laboratory experiments can be described by using the Lambert–Euler omega function as follows:
where H(x) is the debris flow height, x is the channel downstream position, L is the unified model parameter consisting of several physical and geometrical parameters of the flow, flow height and the hydraulic pressure gradient.
Example 10
The Lambert-W function was employed in the field of Neuroimaging for linking cerebral blood flow and oxygen consumption changes within a brain voxel, to the corresponding Blood Oxygenation Level Dependent (BOLD) signal.
Example 11
The Lambert-W function was employed in the field of Chemical Engineering for modelling the porous electrode film thickness in a glassy carbon based supercapacitor for electrochemical energy storage. The Lambert "W" function turned out to be the exact solution for a gas phase thermal activation process where growth of carbon film and combustion of the same film compete with each other.
Example 12
The Lambert-W function was employed in the field of epitaxial film growth for the determination of the critical dislocation onset film thickness. This is the calculated thickness of an epitaxial film, where due to thermodynamic principles the film will develop crystallographic dislocations in order to minimise the elastic energy stored in the films. Prior to application of Lambert "W" for this problem, the critical thickness had to be determined via solving an implicit equation. Lambert "W" turns it in an explicit equation for analytical handling with ease.
Example 13
The Lambert-W function has been employed in the field of fluid flow in porous media to model the tilt of an interface separating two gravitationally segregated fluids in a homogeneus tilted porous bed of constant dip and thickness where the heavier fluid, injected at the bottom end, displaces the lighter fluid that is produced at the same rate from the top end. The principal branch of the solution corresponds to stable displacements while the -1 branch applies if the displacement is unstable with the heavier fluid running underneath the ligther fluid.
Example 14
The equation (linked with the generating functions of Bernoulli numbers and Todd genus):
can be solved by means of the two real branches
This application shows in evidence that the branch difference of the W function can be employed in order to solve other trascendental equations.
See : D. J. Jeffrey and J. E. Jankowski, "Branch differences and Lambert W"
Example 15
The centroid of a set of histograms defined with respect to the symmetrized Kullback-Leibler divergence (also called the Jeffreys divergence) is in closed form using the Lambert function.
See : F. Nielsen, "Jeffreys Centroids: A Closed-Form Expression for Positive Histograms and a Guaranteed Tight Approximation for Frequency Histograms"
Example 16
The Lambert-W function appears in a quantum-mechanical potential (see The Lambert-W step-potential) which affords the fifth – next to those of the harmonic oscillator plus centrifugal, the Coulomb plus inverse square, the Morse, and the inverse square root potential – exact solution to the stationary one-dimensional Schrödinger equation in terms of the confluent hypergeometric functions. The potential is given as
A peculiarity of the solution is that each of the two fundamental solutions that compose the general solution of the Schrödinger equation is given by a combination of two confluent hypergeometric functions of an argument proportional to
See : A.M. Ishkhanyan, "The Lambert W-barrier – an exactly solvable confluent hypergeometric potential"
Generalizations
The standard Lambert-W function expresses exact solutions to transcendental algebraic equations (in x) of the form:
where a0, c and r are real constants. The solution is
Applications of the Lambert "W" function in fundamental physical problems are not exhausted even for the standard case expressed in (1) as seen recently in the area of atomic, molecular, and optical physics.
Plots
Numerical evaluation
The W function may be approximated using Newton's method, with successive approximations to
The W function may also be approximated using Halley's method,
given in Corless et al. to compute W.
Software
The Lambert-W function is implemented as LambertW in Maple, lambertw in GP (and glambertW in PARI), lambertw in MATLAB, also lambertw in octave with the 'specfun' package, as lambert_w in Maxima, as ProductLog (with a silent alias LambertW) in Mathematica, as lambertw in Python scipy's special function package, as LambertW in Perl's ntheory module, and as gsl_sf_lambert_W0 and gsl_sf_lambert_Wm1 functions in special functions section of the GNU Scientific Library – GSL.
