Lambda CDM model

Overview

Most modern cosmological models are based on the cosmological principle, which states that our observational location in the universe is not unusual or special; on a large-enough scale, the universe looks the same in all directions (isotropy) and from every location (homogeneity).

The model includes an expansion of metric space that is well documented both as the red shift of prominent spectral absorption or emission lines in the light from distant galaxies and as the time dilation in the light decay of supernova luminosity curves. Both effects are attributed to a Doppler shift in electromagnetic radiation as it travels across expanding space. Although this expansion increases the distance between objects that are not under shared gravitational influence, it does not increase the size of the objects (e.g. galaxies) in space. It also allows for distant galaxies to recede from each other at speeds greater than the speed of light; local expansion is less than the speed of light, but expansion summed across great distances can collectively exceed the speed of light.

The letter Λ (lambda) represents the cosmological constant, which is currently associated with a vacuum energy or dark energy in empty space that is used to explain the contemporary accelerating expansion of space against the attractive effects of gravity. A cosmological constant has negative pressure, p = − ρ c 2 , which contributes to the stress-energy tensor that, according to the general theory of relativity, causes accelerating expansion. The fraction of the total energy density of our (flat or almost flat) universe that is dark energy, Ω Λ , is currently [2015] estimated to be 69.2 ± 1.2% based on Planck satellite data.

Cold dark matter is a form of matter introduced in order to account for gravitational effects observed in very large-scale structures (the "flat" rotation curves of galaxies; the gravitational lensing of light by galaxy clusters; and enhanced clustering of galaxies) that cannot be accounted for by the quantity of observed matter. Dark matter is described as being cold (i.e. its velocity is far less than the speed of light at the epoch of radiation-matter equality); non-baryonic (i.e. consisting of matter other than protons and neutrons); dissipationless (i.e. cannot cool by radiating photons); and collisionless (i.e. the dark matter particles interact with each other and other particles only through gravity and possibly the weak force). The dark matter component is currently [2013] estimated to constitute about 26.8% of the mass-energy density of the universe.

The remaining 4.9% [2013] comprises all ordinary matter observed as atoms, chemical elements, gas and plasma, the stuff of which visible planets, stars and galaxies are made. As a matter of fact, the great majority of ordinary matter in the universe is unseen, since visible stars and gas inside galaxies and clusters account for less than 10 per cent of the ordinary matter contribution to the mass-energy density of the universe.

Also, the energy density includes a very small fraction (~ 0.01%) in cosmic microwave background radiation, and not more than 0.5% in relic neutrinos. Although very small today, these were much more important in the distant past, dominating the matter at redshift > 3200.

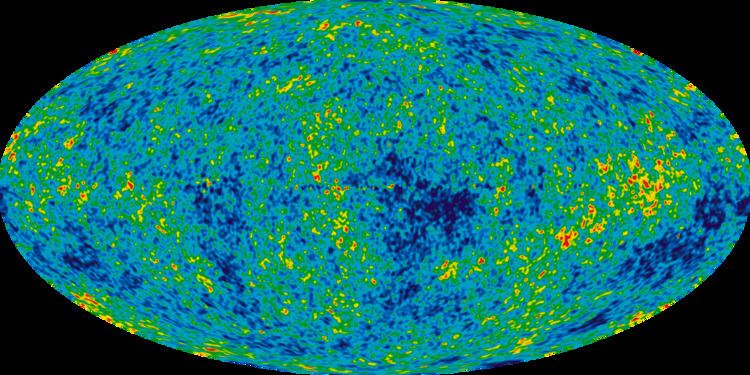
The model includes a single originating event, the "Big Bang", which was not an explosion but the abrupt appearance of expanding space-time containing radiation at temperatures of around 10¹⁵ K. This was immediately (within 10⁻²⁹ seconds) followed by an exponential expansion of space by a scale multiplier of 10²⁷ or more, known as cosmic inflation. The early universe remained hot (above 10,000 K) for several hundred thousand years, a state that is detectable as a residual cosmic microwave background, or CMB, a very low energy radiation emanating from all parts of the sky. The "Big Bang" scenario, with cosmic inflation and standard particle physics, is the only current cosmological model consistent with the observed continuing expansion of space, the observed distribution of lighter elements in the universe (hydrogen, helium, and lithium), and the spatial texture of minute irregularities (anisotropies) in the CMB radiation. Cosmic inflation also addresses the "horizon problem" in the CMB; indeed, it seems likely that the universe is larger than the observable particle horizon.

The model uses the FLRW metric, the Friedmann equations and the cosmological equations of state to describe the observable universe from right after the inflationary epoch to present and future.

Cosmic expansion history

The expansion of the universe is parametrized by a dimensionless scale factor a = a ( t ) (with time t counted from the birth of the universe), defined relative to the present day, so a 0 = a ( t 0 ) = 1 ; the usual convention in cosmology is that subscript 0 denotes present-day values, so t 0 is the current age of the universe. The scale factor is related to the observed redshift z of the light emitted at time t e m by

The expansion rate is described by the time-dependent Hubble parameter, H ( t ) , defined as

where a ˙ is the time-derivative of the scale factor. The first Friedmann equation gives the expansion rate in terms of the matter+radiation density ρ , the curvature k , the cosmological constant Λ , and the gravitational constant G :

A critical density ρ c r i t is the present-day density, which gives zero curvature k , assuming the cosmological constant Λ is zero, regardless of its actual value. Substituting these conditions to the Friedmann equation gives

where h ≡ H 0 / ( 100 k m s − 1 M p c − 1 ) is the reduced Hubble constant. If the cosmological constant were actually zero, the critical density would also be the dividing line between eventual recollapse of the universe to a Big Crunch, or unlimited expansion. Because it is not, the universe is predicted to expand forever regardless of whether the total density is slightly above or below the critical density, though this may not apply if the cosmological constant is time-dependent.

It is standard to define the present-day density parameter Ω x for various species as the dimensionless ratio

where the subscript x is one of "b" for baryons, "c" for cold dark matter, "rad" for radiation (photons plus relativistic neutrinos), and "DE" or "Λ" for dark energy.

Since the densities of various species scale as different powers of a , e.g. a − 3 for matter etc., the Friedmann equation can be conveniently rewritten in terms of the various density parameters as

where w is the equation of state of dark energy, and assuming negligible neutrino mass (significant neutrino mass requires a more complex equation). The various Ω parameters add up to 1 by construction. In the general case this is integrated by computer to give the expansion history a(t) and also observable distance-redshift relations for any chosen values of the cosmological parameters, which can then be compared with observations such as supernovae and baryon acoustic oscillations.

In the minimal 6-parameter Lambda-CDM model, it is assumed that curvature Ω k is zero and w = − 1 , so this simplifies to

Observations show that the radiation density is very small today, Ω r a d ∼ 10 − 4 ; if this term is neglected the above has an analytic solution

where t Λ ≡ 2 / ( 3 H 0 Ω Λ )   ; this is fairly accurate for a > 0.01 or t > 10 Myr. Solving for a ( t ) = 1 gives the present age of the universe t 0 in terms of the other parameters.

It follows that the transition from decelerating to accelerating expansion (the second derivative a ¨ crossing zero) occurred when

which evaluates to a ~ 0.6 or z ~ 0.66 for the Planck best-fit parameters.

Historical development

The discovery of the Cosmic Microwave Background (CMB) in 1965 confirmed a key prediction of the Big Bang cosmology. From that point on, it was generally accepted that the universe started in a hot, dense state and has been expanding over time. The rate of expansion depends on the types of matter and energy present in the universe, and in particular, whether the total density is above or below the so-called critical density. During the 1970s, most attention focused on pure-baryonic models, but there were serious challenges explaining the formation of galaxies, given the small anisotropies in the CMB (upper limits at that time). In the early 1980s, it was realized that this could be resolved if cold dark matter dominated over the baryons, and the theory of cosmic inflation motivated models with critical density. During the 1980s, most research focused on cold dark matter with critical density in matter, around 95% CDM and 5% baryons: these showed success at forming galaxies and clusters of galaxies, but problems remained; notably, the model required a Hubble constant lower than preferred by observations, and observations around 1988-1990 showed more large-scale galaxy clustering than predicted. These difficulties sharpened with the discovery of CMB anisotropy by COBE in 1992, and several modified CDM models, including ΛCDM and mixed cold+hot dark matter, came under active consideration through the mid-1990s. The ΛCDM model then became the leading model following the observations of accelerating expansion in 1998, and was quickly supported by other observations: in 2000, the BOOMERanG microwave background experiment measured the total (matter+energy) density to be close to 100% of critical, whereas in 2001 the 2dFGRS galaxy redshift survey measured the matter density to be near 25%; the large difference between these values supports a positive Λ or dark energy. Much more precise spacecraft measurements of the microwave background from WMAP in 2003 – 2010 and Planck in 2013 - 2015 have continued to support the model and pin down the parameter values, most of which are now constrained below 1 percent uncertainty.

There is currently active research into many aspects of the ΛCDM model, both to refine the parameters and possibly detect deviations. In addition, ΛCDM has no explicit physical theory for the origin or physical nature of dark matter or dark energy; the nearly scale-invariant spectrum of the CMB perturbations, and their image across the celestial sphere, are believed to result from very small thermal and acoustic irregularities at the point of recombination. A large majority of astronomers and astrophysicists support the ΛCDM model or close relatives of it, but Milgrom, McGaugh, and Kroupa are leading critics, attacking the dark matter portions of the theory from the perspective of galaxy formation models and supporting the alternative MOND theory, which requires a modification of the Einstein field equations and the Friedmann equations as seen in proposals such as MOG theory or TeVeS theory. Other proposals by theoretical astrophysicists of cosmological alternatives to Einstein's general relativity that attempt to account for dark energy or dark matter include f(R) gravity, scalar–tensor theories such as galileon theories, brane cosmologies, the DGP model, and massive gravity and its extensions such as bimetric gravity.

Successes

In addition to explaining pre-2000 observations, the model has made a number of successful predictions: notably the existence of the baryon acoustic oscillation feature, discovered in 2005 in the predicted location; and the statistics of weak gravitational lensing, first observed in 2000 by several teams. The polarization of the CMB, discovered in 2002 by DASI is now a dramatic success: in the 2015 Planck data release, there are seven observed peaks in the temperature (TT) power spectrum, six peaks in the temperature-polarization (TE) cross spectrum, and five peaks in the polarization (EE) spectrum, and all well fit by Lambda-CDM.

Challenges

Extensive searches for dark matter particles have so far shown no well-agreed detection; the dark energy may be almost impossible to detect in a laboratory, and its value is unnaturally small compared to naive theoretical predictions.

Comparison of the model with observations is very successful on large scales (larger than galaxies, up to the observable horizon), but may have some problems on sub-galaxy scales, possibly predicting too many dwarf galaxies and too much dark matter in the innermost regions of galaxies. These small scales are harder to resolve in computer simulations, so it is not yet clear whether the problem is the simulations, non-standard properties of dark matter, or a more radical error in the model.

Parameters

The simple ΛCDM model is based on six parameters: physical baryon density parameter; physical dark matter density parameter; the age of the universe; scalar spectral index; curvature fluctuation amplitude; and reionization optical depth. In accordance with Occam's razor, six is the smallest number of parameters needed to give an acceptable fit to current observations; other possible parameters are fixed at "natural" values, e.g. total density parameter = 1.00, dark energy equation of state = −1. (See below for extended models that allow these to vary.)

The values of these six parameters are mostly not predicted by current theory (though, ideally, they may be related by a future "Theory of Everything"), except that most versions of cosmic inflation predict the scalar spectral index should be slightly smaller than 1, consistent with the estimated value 0.96. The parameter values, and uncertainties, are estimated using large computer searches to locate the region of parameter space providing an acceptable match to cosmological observations. From these six parameters, the other model values, such as the Hubble constant and the dark energy density, can be readily calculated.

Commonly, the set of observations fitted includes the cosmic microwave background anisotropy, the brightness/redshift relation for supernovae, and large-scale galaxy clustering including the baryon acoustic oscillation feature. Other observations, such as the Hubble constant, the abundance of galaxy clusters, weak gravitational lensing and globular cluster ages, are generally consistent with these, providing a check of the model, but are less precisely measured at present.

Parameter values listed below are from the Planck Collaboration Cosmological parameters 68% confidence limits for the base ΛCDM model from Planck CMB power spectra, in combination with lensing reconstruction and external data (BAO+JLA+H₀). See also Planck (spacecraft).

Extended models

Extended models allow one or more of the "fixed" parameters above to vary, in addition to the basic six; so these models join smoothly to the basic six-parameter model in the limit that the additional parameter(s) approach the default values. For example, possible extensions of the simplest ΛCDM model allow for spatial curvature (Ω_tot may be different from 1); or quintessence rather than a cosmological constant where the equation of state of dark energy is allowed to differ from −1. Cosmic inflation predicts tensor fluctuations (gravitational waves). Their amplitude is parameterized by the tensor-to-scalar ratio (denoted r), which is determined by the unknown energy scale of inflation. Other modifications allow hot dark matter in the form of neutrinos more massive than the minimal value, or a running spectral index; the latter is generally not favoured by simple cosmic inflation models.

Allowing additional variable parameter(s) will generally increase the uncertainties in the standard six parameters quoted above, and may also shift the central values slightly. The Table below shows results for each of the possible "6+1" scenarios with one additional variable parameter; this indicates that, as of 2015, there is no convincing evidence that any additional parameter is different from its default value.

Some researchers have suggested that there is a running spectral index, but no statistically significant study has revealed one. Theoretical expectations suggest that the tensor-to-scalar ratio r should be between 0 and 0.3, and the latest results are now within those limits.