Katapayadi system

History

The oldest available evidence of the use of Kaṭapayādi (Sanskrit: कटपयादि) system is from Grahacāraṇibandhana by Haridatta in 683 CE. It has been used in Laghu·bhāskarīya·vivaraṇa written by Śaṅkara·nārāyaṇa in 869 CE.

Some argue that the system originated from Vararuci. In some astronomical texts popular in Kerala planetary positions were encoded in the Kaṭapayādi system. The first such work is considered to be the Chandra-vakyani of Vararuci, who is traditionally assigned to the fourth century CE. Therefore, sometime in the early first millennium is a reasonable estimate for the origin of the Kaṭapayādi system.

Aryabhata, in his treatise Ārya·bhaṭīya, is known to have used a similar, more complex system to represent astronomical numbers. There is no definitive evidence whether the Ka-ṭa-pa-yā-di system originated from Āryabhaṭa numeration.

Geographical spread of the use

Almost all evidences of the use of Ka-ṭa-pa-yā-di system is from south India, especially Kerala. Not much is known about its use in north India. However, on a Sanskrit astrolabe discovered in north India, the degrees of the altitude are marked in the Kaṭapayādi system. It is preserved in the Sarasvathy Bhavan Library of Sampurnanand Sanskrit University, Varanasi.

The Ka-ṭa-pa-yā-di system is not confined to India. Some Pali chronograms based on the Ka-ṭa-pa-yā-di system have been discovered in Burma.

Rules and practices

Following verse found in Śaṅkaravarman's Sadratnamāla explains the mechanism of the system.

नज्ञावचश्च शून्यानि संख्या: कटपयादय:।
मिश्रे तूपान्त्यहल् संख्या न च चिन्त्यो हलस्वर:॥

Transiliteration:

nanyāvacaśca śūnyāni saṃkhyāḥ kaṭapayādayaḥ
miśre tūpāntyahal saṃkhyā na ca cintyo halasvaraḥ

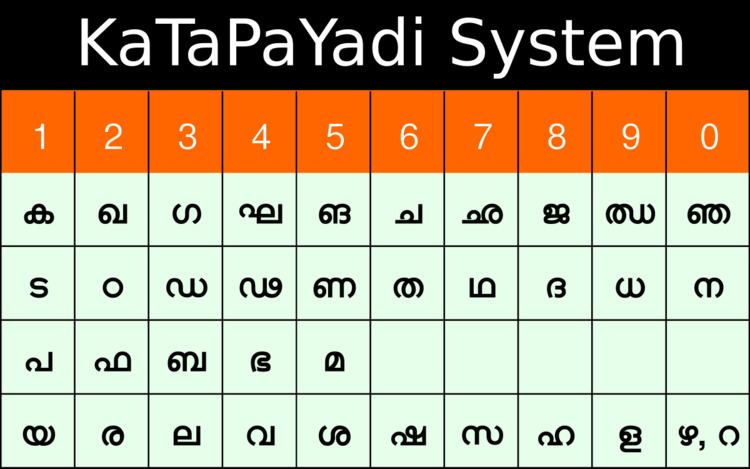
Translation: na (न), nya (ञ) and a (अ)-s, i.e., vowels represent zero. The nine integers are represented by consonant group beginning with ka, ṭa, pa, ya. In a conjunct consonant, the last of the consonants alone will count. A consonant without vowel is to be ignored.

Explanation: The assignment of letters to the numerals are as per the following arrangement.

Consonants have numerals assigned as per the above table. For example, ba (ब) is always 3 whereas 5 can be represented by either nga (ङ) or ṇa (ण) or ma (म) or śha (श).

All stand-alone vowels like a (अ) and ṛ (ऋ) are assigned to zero.

In case of a conjunct, consonants attached to a non-vowel will not be valueless. For example, kya (क्या) is formed by k (क्) + ya (य) + a (अ). The only consonant standing with a vowel is ya (य). So the corresponding numeral for kya (क्या) will be 1.

There is no way of representing Decimal separator in the system.

Indians used the Hindu-Arabic numeral system for numbering, traditionally written in increasing place values from left to right. This is as per the rule aṅkānām vāmato gatiḥ (अङ्कानाम् वामतो गतिः) which means numbers go from left to right.

Variations

The consonant, ḷ (Malayālam: ള, Devanāgarī: ळ), present in the Dravidian languages of south India, is employed in works using the Kaṭapayādi system, like Mādhava's sine table.

Some practitioners do not map the stand-alone vowels to zero. But, it is sometimes considered valueless.

Mathematics and astronomy

Mādhava's sine table constructed by 14th century Kerala mathematician-astronomer Mādhava of Saṅgama·grāma employs the Kaṭapayādi system to enlist the trigonometric sines of angles.

Karaṇa·paddhati, written in the 15th century, has the following śloka for the value of pi (π)

Transliteration

vyāsastadarddhaṃ tribhamaurvika syāt

It gives the circumference of a circle of diameter, anūnanūnnānananunnanityai (10,000,000,000) as caṇḍāṃśucandrādhamakuṃbhipālair (31415926536).

Śaṅkara·varman's Sad·ratna·mālā uses the Kaṭapayādi system. A famous verse found in Sad·ratna·mālā is

TransliterationSplitting the consonants gives,Reversing the digits to modern day usage of descending order of decimal places, we get 314159265358979324 which is the value of pi (π) to 17 decimal places, except the last digit might be rounded off to 4.

This verse encrypts the value of pi (π) up to 31 decimal places.

गोपीभाग्यमधुव्रात-श्रुग्ङिशोदधिसन्धिग ॥ खलजीवितखाताव गलहालारसंधर ॥ ಗೋಪೀಭಾಗ್ಯಮಧುವ್ರಾತ-ಶ್ರುಂಗಿಶೋದಧಿಸಂಧಿಗ || ಖಲಜೀವಿತಖಾತಾವ ಗಲಹಾಲಾರಸಂಧರ ||

This verse directly yields the decimal equivalent of pi divided by 10: pi/10 = 0.31415926535897932384626433832792

గోపీభాగ్యమధువ్రాత-శృంగిశోదధిసంధిగ | ఖలజీవితఖాతావ గలహాలారసంధర ||

Carnatic music

The melakarta ragas of the Carnatic music is named so that the first two syllables of the name will give its number. This system is sometimes called the Ka-ta-pa-ya-di sankhya. The Swaras 'Sa' and 'Pa' are fixed, and here is how to get the other swaras from the melakarta number.

1. Melakartas 1 through 36 have Ma1 and those from 37 through 72 have Ma2.
2. The other notes are derived by noting the (integral part of the) quotient and remainder when one less than the melakarta number is divided by 6.
3. 'Ri' and 'Ga' positions: the raga will have:
4. Ri1 and Ga1 if the quotient is 0
5. Ri1 and Ga2 if the quotient is 1
6. Ri1 and Ga3 if the quotient is 2
7. Ri2 and Ga2 if the quotient is 3
8. Ri2 and Ga3 if the quotient is 4
9. Ri3 and Ga3 if the quotient is 5
10. 'Da' and 'Ni' positions: the raga will have:
11. Da1 and Ni1 if remainder is 0
12. Da1 and Ni2 if remainder is 1
13. Da1 and Ni3 if remainder is 2
14. Da2 and Ni2 if remainder is 3
15. Da2 and Ni3 if remainder is 4
16. Da3 and Ni3 if remainder is 5

See swaras in Carnatic music for details on above notation.

Raga Dheerasankarabharanam

The katapayadi scheme associates dha ↔ 9 and ra ↔ 2, hence the raga's melakarta number is 29 (92 reversed). Now 29 ≤ 36, hence Dheerasankarabharanam has Ma1. Divide 28 (1 less than 29) by 6, the quotient is 4 and the remainder 4. Therefore, this raga has Ri2, Ga3 (quotient is 4) and Da2, Ni3 (remainder is 4). Therefore, this raga's scale is Sa Ri2 Ga3 Ma1 Pa Da2 Ni3 SA.

Raga MechaKalyani

From the coding scheme Ma ↔ 5, Cha ↔ 6. Hence the raga's melakarta number is 65 (56 reversed). 65 is greater than 36. So MechaKalyani has Ma2. Since the raga's number is greater than 36 subtract 36 from it. 65-36=29. 28 (1 less than 29) divided by 6: quotient=4, remainder=4. Ri2 Ga3 occurs. Da2 Ni3 occurs. So MechaKalyani has the notes Sa Ri2 Ga3 Ma2 Pa Da2 Ni3 SA.

Exception for Simhendramadhyamam

As per the above calculation, we should get Sa ↔ 7, Ha ↔ 8 giving the number 87 instead of 57 for Simhendramadhyamam. This should be ideally Sa ↔ 7, Ma ↔ 5 giving the number 57. So it is believed that the name should be written as Sihmendramadhyamam (as in the case of Brahmana in Sanskrit).

Representation of dates

Important dates were remembered by converting them using Kaṭapayādi system. These dates are generally represented as number of days since the start of Kali Yuga. It is sometimes called kalidina sankhya.

The Malayalam calendar known as kollavarsham (Malayalam: കൊല്ലവര്‍ഷം) was adopted in Kerala beginning from 825 CE, revamping some calendars. This date is remembered as āchārya vāgbhadā, converted using Kaṭapayādi into 1434160 days since the start of Kali Yuga.

Narayaniyam, written by Melpathur Narayana Bhattathiri, ends with the line, āyurārogyasaukhyam (ആയുരാരോഗ്യസൌഖ്യം) which means long-life, health and happiness.

This number is the time at which the work was completed represented as number of days since the start of Kali Yuga as per the Malayalam calendar.

Others

Some people use the Kaṭapayādi system in naming newborns.

The following verse compiled in Malayalam by Koduṅṅallur Kuññikkuṭṭan Taṃpurān using Kaṭapayādi is the number of days in the months of Gregorian Calendar.

TransiliterationTranslation: Milk is best for breakfast, when it is morning, it should be stirred. But Gopālan says there is no milk - the number of days of English months in order.Converting pairs of letters using Kaṭapayādi yields - pala (പല) is 31, hāre (ഹാരേ) is 28, pālu പാലു = 31, nallū (നല്ലൂ) is 30, pular (പുലര്‍) is 31, nnālo (ന്നാലോ) is 30, kala (കല) is 31, kkilāṃ (ക്കിലാം) is 31, illā (ഇല്ലാ) is 30, pāle (പാലെ) is 31, nnu go (ന്നു ഗോ) is 30, pālan (പാലന്‍) is 31.