Karush–Kuhn–Tucker conditions

Nonlinear optimization problem

Consider the following nonlinear optimization problem:

Minimize f ( x ) subject to

where x is the optimization variable, f is the objective or utility function, g i   ( i = 1 , … , m ) are the inequality constraint functions, and h j   ( j = 1 , … , ℓ ) are the equality constraint functions. The numbers of inequality and equality constraints are denoted m and ℓ, respectively.

Necessary conditions

Suppose that the objective function f : R n → R and the constraint functions g i : R n → R and h j : R n → R are continuously differentiable at a point x ∗ . If x ∗ is a local optimum and the optimization problem satisfies some regularity conditions (see below), then there exist constants μ i   ( i = 1 , … , m ) and λ j   ( j = 1 , … , ℓ ) , called KKT multipliers, such that

Stationarity

For maximizing f(x): ∇ f ( x ∗ ) = ∑ i = 1 m μ i ∇ g i ( x ∗ ) + ∑ j = 1 ℓ λ j ∇ h j ( x ∗ ) , For minimizing f(x): − ∇ f ( x ∗ ) = ∑ i = 1 m μ i ∇ g i ( x ∗ ) + ∑ j = 1 ℓ λ j ∇ h j ( x ∗ ) ,

Primal feasibility

g i ( x ∗ ) ≤ 0 ,  for  i = 1 , … , m h j ( x ∗ ) = 0 ,  for  j = 1 , … , ℓ

Dual feasibility

μ i ≥ 0 ,  for  i = 1 , … , m

Complementary slackness

μ i g i ( x ∗ ) = 0 ,  for  i = 1 , … , m .

In the particular case m = 0 , i.e., when there are no inequality constraints, the KKT conditions turn into the Lagrange conditions, and the KKT multipliers are called Lagrange multipliers.

If some of the functions are non-differentiable, subdifferential versions of Karush–Kuhn–Tucker (KKT) conditions are available.

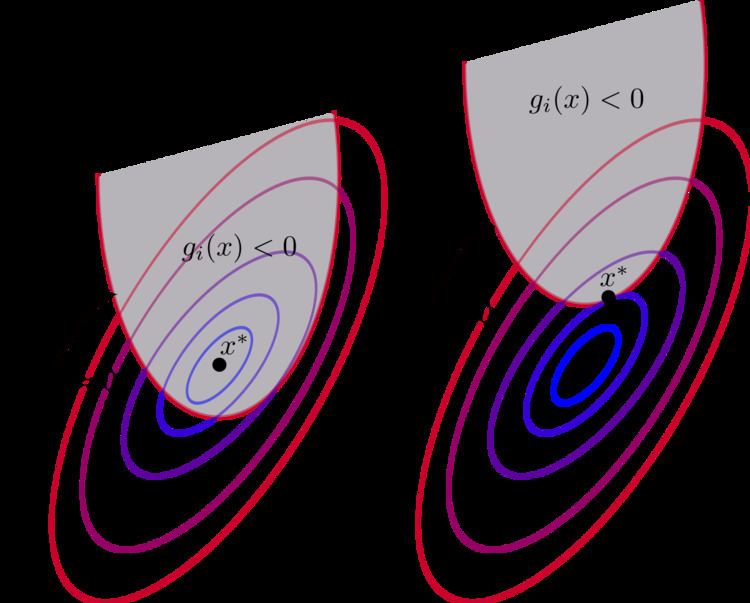
Regularity conditions (or constraint qualifications)

In order for a minimum point x ∗ to satisfy the above KKT conditions, the problem should satisfy some regularity conditions; some common examples are tabulated here:

( v 1 , … , v n ) is positive-linear dependent if there exists a 1 ≥ 0 , … , a n ≥ 0 not all zero such that a 1 v 1 + ⋯ + a n v n = 0 .

It can be shown that

LICQ⇒MFCQ⇒CPLD⇒QNCQ

and

LICQ⇒CRCQ⇒CPLD⇒QNCQ

(and the converses are not true), although MFCQ is not equivalent to CRCQ. In practice weaker constraint qualifications are preferred since they provide stronger optimality conditions.

Sufficient conditions

In some cases, the necessary conditions are also sufficient for optimality. In general, the necessary conditions are not sufficient for optimality and additional information is necessary, such as the Second Order Sufficient Conditions (SOSC). For smooth functions, SOSC involve the second derivatives, which explains its name.

The necessary conditions are sufficient for optimality if the objective function f of a maximization problem is a concave function, the inequality constraints g j are continuously differentiable convex functions and the equality constraints h i are affine functions.

It was shown by Martin in 1985 that the broader class of functions in which KKT conditions guarantees global optimality are the so-called Type 1 invex functions.

Second-order sufficient conditions

For smooth, non-linear optimisation problems, a second order sufficient condition is given as follows. Consider x ∗ , λ ∗ , ρ ∗ that find a local minimum using the Karush–Kuhn–Tucker conditions above. With ρ ∗ such that strict complementarity is held at x ∗ (i.e. all ρ i > 0 ), then for all s ≠ 0 such that

[ ∂ g ( x ∗ ) ∂ x , ∂ h ( x ∗ ) ∂ x ] T s = 0

the following equation must hold;

s ′ ∇ x x 2 L ( x ∗ , λ ∗ , ρ ∗ ) s ≥ 0

If the above condition is strictly met, the function is a strict constrained local minimum.

Economics

Often in mathematical economics the KKT approach is used in theoretical models in order to obtain qualitative results. For example, consider a firm that maximizes its sales revenue subject to a minimum profit constraint. Letting Q be the quantity of output produced (to be chosen), R(Q) be sales revenue with a positive first derivative and with a zero value at zero output, C(Q) be production costs with a positive first derivative and with a non-negative value at zero output, and G min be the positive minimal acceptable level of profit, then the problem is a meaningful one if the revenue function levels off so it eventually is less steep than the cost function. The problem expressed in the previously given minimization form is

Minimize − R ( Q ) subject to G min ≤ R ( Q ) − C ( Q ) Q ≥ 0 ,

and the KKT conditions are

( d R / d Q ) ( 1 + μ ) − μ ( d C / d Q ) ≤ 0 , Q ≥ 0 , Q [ ( d R / d Q ) ( 1 + μ ) − μ ( d C / d Q ) ] = 0 , R ( Q ) − C ( Q ) − G min ≥ 0 , μ ≥ 0 , μ [ R ( Q ) − C ( Q ) − G min ] = 0.

Since Q = 0 would violate the minimum profit constraint, we have Q > 0 and hence the third condition implies that the first condition holds with equality. Solving that equality gives

d R / d Q = μ 1 + μ ( d C / d Q ) .

Because it was given that d R / d Q and d C / d Q are strictly positive, this inequality along with the non-negativity condition on μ guarantees that μ is positive and so the revenue-maximizing firm operates at a level of output at which marginal revenue d R / d Q is less than marginal cost d C / d Q — a result that is of interest because it contrasts with the behavior of a profit maximizing firm, which operates at a level at which they are equal.

Value function

If we reconsider the optimization problem as a maximization problem with constant inequality constraints,v.

Maximize  f ( x ) subject to   

The value function is defined as

V ( a 1 , … , a n ) = sup x f ( x ) subject to   

(So the domain of V is { a ∈ R m ∣ for some  x ∈ X , g i ( x ) ≤ a i , i ∈ { 1 , … , m } . )

Given this definition, each coefficient, μ i , is the rate at which the value function increases as a i increases. Thus if each a i is interpreted as a resource constraint, the coefficients tell you how much increasing a resource will increase the optimum value of our function f. This interpretation is especially important in economics and is used, for instance, in utility maximization problems.

Generalizations

With an extra constant multiplier μ 0 , which may be zero, in front of ∇ f ( x ∗ ) the KKT stationarity conditions turn into

μ 0 ∇ f ( x ∗ ) + ∑ i = 1 m μ i ∇ g i ( x ∗ ) + ∑ j = 1 ℓ λ j ∇ h j ( x ∗ ) = 0 ,

which are called the Fritz John conditions.

The KKT conditions belong to a wider class of the first-order necessary conditions (FONC), which allow for non-smooth functions using subderivatives.