Suvarna Garge (Editor)

KHOPCA clustering algorithm

Updated on
Edit
Like
Comment
Share on FacebookTweet on TwitterShare on LinkedInShare on Reddit
KHOPCA clustering algorithm

KHOPCA is a clustering algorithm designed for dynamic networks. KHOPCA ( k -hop clustering algorithm) provides a fully distributed and localized approach to group elements such as nodes in a network according to their distance from each other. KHOPCA operates proactively through a simple set of rules that defines clusters, which are optimal with respect to the applied distance function.

Contents

KHOPCA's clustering process explicitly supports joining and leaving of nodes, which makes KHOPCA suitable for highly dynamic networks. However, it has been demonstrated that KHOPCA also performs in static networks.

Besides applications in ad hoc and wireless sensor networks, KHOPCA can be used in localization and navigation problems, networked swarming, and real-time data clustering and analysis.

Algorithm description

KHOPCA ( k -hop clustering algorithm) operates proactively through a simple set of rules that defines clusters with variable k -hops. A set of local rules describes the state transition between nodes. A node's weight is determined only depending on the current state of its neighbors in communication range. Each node of the network is continuously involved in this process. As result, k -hop clusters are formed and maintained in static as well as dynamic networks.

KHOPCA does not require any predetermined initial configuration. Therefore, a node can potentially choose any weight (between M I N and M A X ). However, the choice of the initial configuration does influence the convergence time.

Initialization

The prerequisites in the start configuration for the application of the rules are the following.

  • N is the network with nodes and links, whereby each node has a weight w .
  • Each node n in N node stores the same positive values M I N and M A X , with M I N < M A X .
  • A node n with weight w n = M A X is called cluster center.
  • k is M A X - M I N and represents the maximum size a cluster can have from the most outer node to the cluster center. The cluster diameter is therefore k ⋅ 2 − 1 .
  • N ( n ) returns the direct neighbors of node n .
  • W ( N ) is the set of weights of all nodes of N .

    • The following rules describe the state transition for a node n with weight w n . These rules have to be executed on each node in the order described here.

    Rule 1

    The first rule has the function of constructing an order within the cluster. This happens through a node n detects the direct neighbor with the highest weight w , which is higher than the node's own weight w n . If such a direct neighbor is detected, the node n changes its own weight to be the weight of the highest weight within the neighborhood subtracted by 1. Applied iteratively, this process creates a top-to-down hierarchical cluster structure.

    Rule 2

    The second rule deals with the situation where nodes in a neighborhood are on the minimum weight level. This situation can happen if, for instance, the initial configuration assigns the minimum weight to all nodes. If there is a neighborhood with all nodes having the minimum weight level, the node n declares itself as cluster center. Even if coincidently all nodes declare themselves as cluster centers, the conflict situation will be resolved by one of the other rules.

    Rule 3

    The third rule describes situations where nodes with leveraged weight values, which are not cluster centers, attract surrounding nodes with lower weights. This behavior can lead to fragmented clusters without a cluster center. In order to avoid fragmented clusters, the node with higher weight value is supposed to successively decrease its own weight with the objective to correct the fragmentation by allowing the other nodes to reconfigure according to the rules.

    Rule 4

    The fourth rule resolves the situation where two cluster centers connect in 1-hop neighborhood and need to decide which cluster center should continue its role as cluster center. Given any specific criterion (e.g., device ID, battery power), one cluster center remains while the other cluster center is hierarchized in 1-hop neighborhood to that new cluster center. The choice of the specific criterion to resolve the decision-making depends on the used application scenario and on the available information.

    1-D

    An exemplary sequence of state transitions applying the described four rules is illustrated below.

    2-D

    KHOPCA acting in a dynamic 2-D simulation. The geometry is based on a geometric random graph; all existing links are drawn in this network.

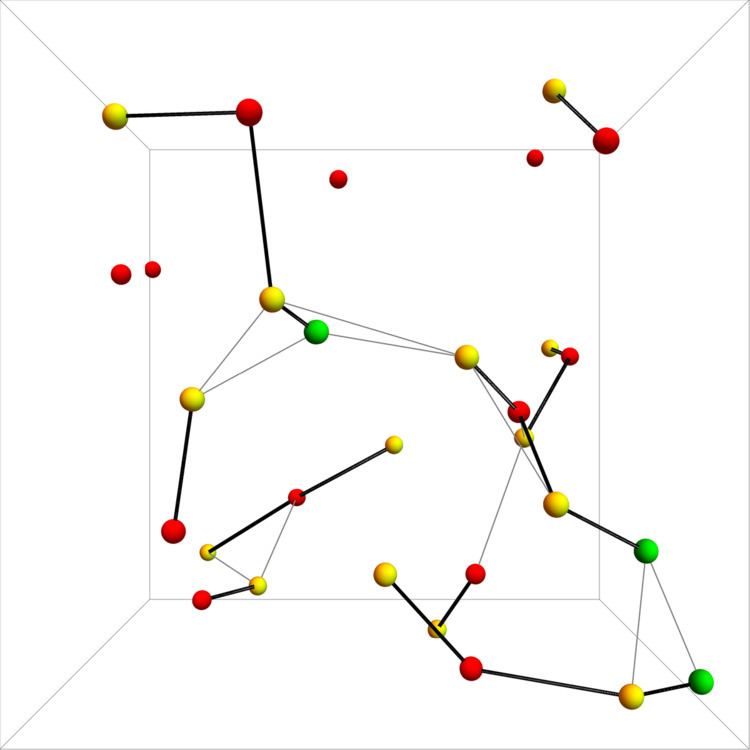
    3-D

    KHOPCA also works in a dynamic 3-D environment. The cluster connections are illustrated with bold lines.

    Guarantees

    It has been demonstrated that KHOPCA terminates after a finite number of state transitions in static networks.

    References

    KHOPCA clustering algorithm Wikipedia
    (Text) CC BY-SA


    Similar Topics