Suvarna Garge (Editor)

Johnson graph

Updated on
Edit
Like
Comment
Share on FacebookTweet on TwitterShare on LinkedInShare on Reddit
Named after
  
Selmer M. Johnson

Johnson graph

Vertices
  
( n k ) {\displaystyle {\binom {n}{k}}}

Edges
  
k ( n − k ) 2 ( n k ) {\displaystyle {\frac {k(n-k)}{2}}{\binom {n}{k}}}

Diameter
  
min ( k , n − k ) {\displaystyle \min(k,n-k)}

Properties
  
( k ( n − k ) ) {\displaystyle (k(n-k))} -regular Vertex-transitive Distance-transitive Hamilton-connected

Notation
  
J ( n , k ) {\displaystyle J(n,k)}

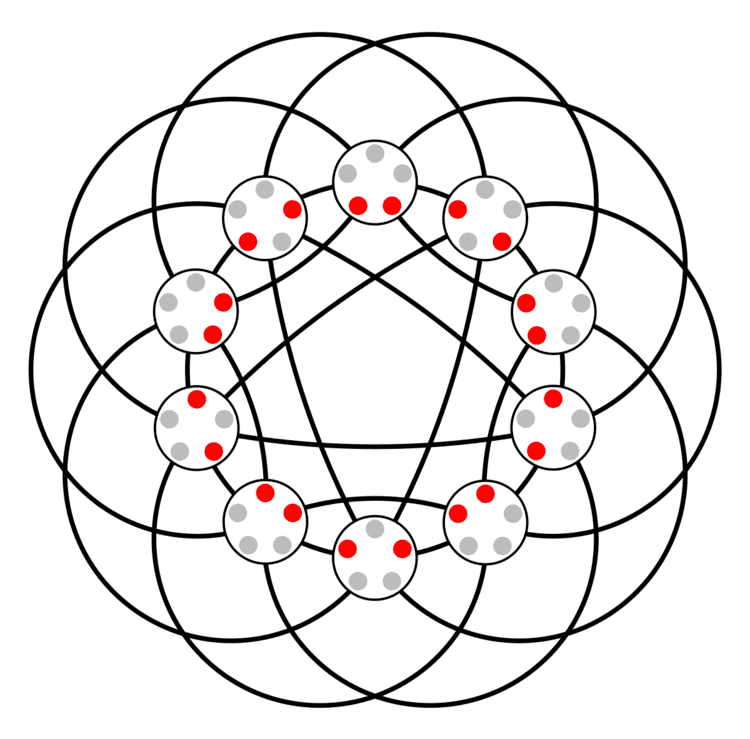
Johnson graphs are a special class of undirected graphs defined from systems of sets. The vertices of the Johnson graph J ( n , k ) are the k -element subsets of an n -element set; two vertices are adjacent when the intersection of the two vertices (subsets) contains ( k − 1 ) -elements. Both Johnson graphs and the closely related Johnson scheme are named after Selmer M. Johnson.

Contents

Special cases

  • J ( n , 1 ) is the complete graph Kn.
  • J ( 4 , 2 ) is the octahedral graph.
  • J ( 5 , 2 ) is the complement graph of the Petersen graph, hence the line graph of K5. More generally, for all n, the Johnson graph J ( n , 2 ) is the complement of the Kneser graph K G ( n , 2 )

    • Properties

    In the Johnson graph, the distance between every two vertices is half of the Hamming distance between the sets corresponding to the vertices. Johnson graphs are distance-transitive graphs: there is a graph automorphism mapping any pair of vertices to any other pair at the same distance.

    As a consequence of being distance-transitive, every Johnson graph is also distance-regular. This means that, for every possible distance d between two vertices in the graph, there is a triple of numbers ( a d , b d , c d ) such that, for every pair ( v , w ) of vertices at distance d from each other, w has exactly a i neighbors at distance d from v , exactly b i neighbors at distance d + 1 from v , and exactly c i neighbors at distance d − 1 from v . These triples of numbers can be grouped into a matrix with one column per distance, called the intersection array of the graph, and this intersection array may be used to classify the distance-transitive graphs. It turns out that the intersection arrays of Johnson graphs are almost always enough to classify them completely: except for J ( 8 , 2 ) , each Johnson graph has an intersection array that is not shared with any other graph. However, the intersection array of J ( 8 , 2 ) is shared with three other distance-regular graphs that are not Johnson graphs.

    Every Johnson graph is Hamilton-connected, meaning that every pair of vertices forms the endpoints of a Hamiltonian path in the graph. In particular this means that it has a Hamiltonian cycle. Every Johnson graph J(n,k) forms the graph of vertices and edges of an (n − 1)-dimensional polytope, called a hypersimplex.

    The eigenvectors of Johnson graph have an explicit description.

    The vertex-expansion properties of Johnson graph, as well as the structure of the corresponding extremal sets of vertices of a given size, are not fully understood. However, an asymptotically tight lower-bound on expansion of large sets of vertices was recently obtained. It is also known that the Johnson graph J ( n , k )   is   k ( n − k ) -vertex-connected.

    Relation to Johnson scheme

    The Johnson graph J ( n , k ) is closely related to the Johnson scheme, an association scheme in which each pair of k-element sets is associated with a number, half the size of the symmetric difference of the two sets. The Johnson graph has an edge for every pair of sets at distance one in the association scheme, and the distances in the association scheme are exactly the shortest path distances in the Johnson graph.

    The Johnson scheme is also related to another family of distance-transitive graphs, the odd graphs, whose vertices are k -element subsets of an ( 2 k + 1 ) -element set and whose edges correspond to disjoint pairs of subsets.

    References

    Johnson graph Wikipedia
    (Text) CC BY-SA