Data structure Graph | ||
 | ||
Worst-case performance O ( E V ) {displaystyle O(E{sqrt {V}})} Worst-case space complexity O ( V ) {displaystyle O(V)} | ||
In computer science, the Hopcroft–Karp algorithm is an algorithm that takes as input a bipartite graph and produces as output a maximum cardinality matching – a set of as many edges as possible with the property that no two edges share an endpoint. It runs in
Contents
- Augmenting paths
- Algorithm
- Analysis
- Comparison with other bipartite matching algorithms
- Non bipartite graphs
- Pseudocode
- Explanation
- References
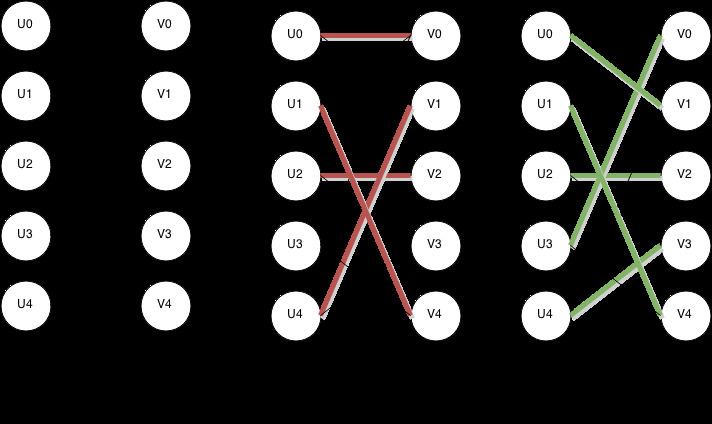
The algorithm was found by John Hopcroft and Richard Karp (1973). As in previous methods for matching such as the Hungarian algorithm and the work of Edmonds (1965), the Hopcroft–Karp algorithm repeatedly increases the size of a partial matching by finding augmenting paths: sequences of edges that alternate between being in and out of the matching, such that swapping which edges of the path are in and which are out of the matching produces a larger matching. However, instead of finding just a single augmenting path per iteration, the algorithm finds a maximal set of shortest augmenting paths. As a result, only
Augmenting paths
A vertex that is not the endpoint of an edge in some partial matching
If
Conversely, suppose that a matching
An augmenting path in a matching problem is closely related to the augmenting paths arising in maximum flow problems, paths along which one may increase the amount of flow between the terminals of the flow. It is possible to transform the bipartite matching problem into a maximum flow instance, such that the alternating paths of the matching problem become augmenting paths of the flow problem. In fact, a generalization of the technique used in Hopcroft–Karp algorithm to arbitrary flow networks is known as Dinic's algorithm.
Algorithm
The algorithm may be expressed in the following pseudocode.
Input: Bipartite graphIn more detail, let
The algorithm terminates when no more augmenting paths are found in the breadth first search part of one of the phases.
Analysis
Each phase consists of a single breadth first search and a single depth first search. Thus, a single phase may be implemented in linear time. Therefore, the first
It can be shown that each phase increases the length of the shortest augmenting path by at least one: the phase finds a maximal set of augmenting paths of the given length, so any remaining augmenting path must be longer. Therefore, once the initial
Since the algorithm performs a total of at most
In many instances, however, the time taken by the algorithm may be even faster than this worst case analysis indicates. For instance, in the average case for sparse bipartite random graphs, Bast et al. (2006) (improving a previous result of Motwani 1994) showed that with high probability all non-optimal matchings have augmenting paths of logarithmic length. As a consequence, for these graphs, the Hopcroft–Karp algorithm takes
Comparison with other bipartite matching algorithms
For sparse graphs, the Hopcroft–Karp algorithm continues to have the best known worst-case performance, but for dense graphs a more recent algorithm by Alt et al. (1991) achieves a slightly better time bound,
Several authors have performed experimental comparisons of bipartite matching algorithms. Their results in general tend to show that the Hopcroft–Karp method is not as good in practice as it is in theory: it is outperformed both by simpler breadth-first and depth-first strategies for finding augmenting paths, and by push-relabel techniques.
Non-bipartite graphs
The same idea of finding a maximal set of shortest augmenting paths works also for finding maximum cardinality matchings in non-bipartite graphs, and for the same reasons the algorithms based on this idea take
Pseudocode
/* G = U ∪ V ∪ {NIL} where U and V are partition of graph and NIL is a special null vertex*/ function BFS () for u in U if Pair_U[u] == NIL Dist[u] = 0 Enqueue(Q,u) else Dist[u] = ∞ Dist[NIL] = ∞ while Empty(Q) == false u = Dequeue(Q) if Dist[u] < Dist[NIL] for each v in Adj[u] if Dist[ Pair_V[v] ] == ∞ Dist[ Pair_V[v] ] = Dist[u] + 1 Enqueue(Q,Pair_V[v]) return Dist[NIL] != ∞function DFS (u) if u != NIL for each v in Adj[u] if Dist[ Pair_V[v] ] == Dist[u] + 1 if DFS(Pair_V[v]) == true Pair_V[v] = u Pair_U[u] = v return true Dist[u] = ∞ return false return truefunction Hopcroft-Karp for each u in U Pair_U[u] = NIL for each v in V Pair_V[v] = NIL matching = 0 while BFS() == true for each u in U if Pair_U[u] == NIL if DFS(u) == true matching = matching + 1 return matchingExplanation
Let our graph have two partitions U, V. The key idea is to add two dummy vertices on each side of the graph: uDummy connecting it to all unmatched vertices in U and vDummy connecting to all unmatched vertices in V. Now if we run BFS from uDummy to vDummy then we can get shortest path between an unmatched vertex in U to unmatched vertex in V. Due to bipartite nature of the graph, this path would zig zag from U to V. However we need to make sure that when going from V to U, we always select matched edge. If there is no matched edge then we end at vDummy. If we make sure of this criteria during BFS then the generated path would meet the criteria for being an augmented shortest path.
Once we have found the augmented shortest path, we want to make sure we ignore any other paths that are longer than this shortest paths. BFS algorithm marks nodes in path with distance with source being 0. Thus, after doing BFS, we can start at each unmatched vertex in U, follow the path by following nodes with distance that increments by 1. When we finally arrive at the destination vDummy, if its distance is 1 more than last node in V then we know that the path we followed is (one of the possibly many) shortest path. In that case we can go ahead and update the pairing for vertices on path in U and V. Note that each vertex in V on path, except for the last one, is non-free vertex. So updating pairing for these vertices in V to different vertices in U is equivalent to removing previously matched edge and adding new unmatched edge in matching. This is same as doing the symmetric difference (i.e. remove edges common to previous matching and add non-common edges in augmented path in new matching).
How do we make sure augmented paths are vertex disjoint? It is already guaranteed: After doing the symmetric difference for a path, none of its vertices could be considered again just because the Dist[ Pair_V[v] ] will not be equal to Dist[u] + 1 (It would be exactly Dist[u]).
So what is the mission of these two lines in pseudocode?:
Dist[u] = ∞return falseWhen we were not able to find any shortest augmented path from a vertex, DFS returns false. In this case it would be good to mark these vertices to not to visit them again. This marking is simply done by setting Dist[u] to infinity.
Finally, we actually don't need uDummy because it's there just to put all unmatched vertices of U in queue when BFS starts. That we can do as just as initialization. The vDummy can be appended in U for convenience in many implementations and initialize default pairing for all V to point to vDummy. That way, if final vertex in V doesn't have any matching vertex in U then we finally end at vDummy which is the end of our augmented path. In above pseudocode vDummy is denoted as Nil.
