Histogram matching

Algorithm

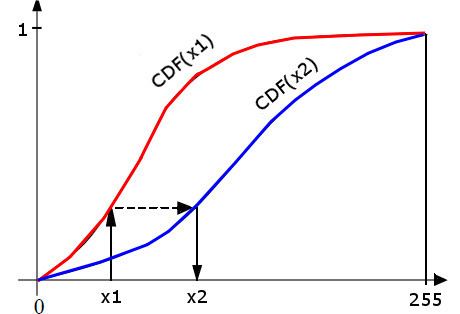
Given two images, the reference and the adjusted images, we compute their histograms. Following, we calculate the cumulative distribution functions of the two images' histograms – F 1 ( ) for the reference image and F 2 ( ) for the target image. Then for each gray level G 1 ∈ [ 0 , 255 ] , we find the gray level G 2 for which F 1 ( G 1 ) = F 2 ( G 2 ) , and this is the result of histogram matching function: M ( G 1 ) = G 2 . Finally, we apply the function M ( ) on each pixel of the reference image.

Exact histogram matching

In typical real-world applications, with 8-bit pixel values (discrete values in range [0, 255]), histogram matching can only approximate the specified histogram. All pixels of a particular value in the original image must be transformed to just one value in the output image.

Exact histogram matching is the problem of finding a transformation for a discrete image so that its histogram exactly matches the specified histogram. Several techniques have been proposed for this. One simplistic approach converts the discrete-valued image into a continuous-valued image and adds small random values to each pixel so their values can be ranked without ties. However, this introduces noise to the output image.

Multiple histogram matching

The histogram matching algorithm can be extended to find a monotonic mapping between two sets of histograms. Given two sets of histograms P = { p i } i = 1 k and Q = { q i } i = 1 k , the optimal monotonic color mapping M is calculated to minimize the distance between the two sets simultaneously, namely arg ⁡ min M   ∑ k d ( M ( p k ) , q k ) where d ( ⋅ , ⋅ ) is a distance metric between two histograms. The optimal solution is calculated using dynamic programming.