Rahul Sharma (Editor)

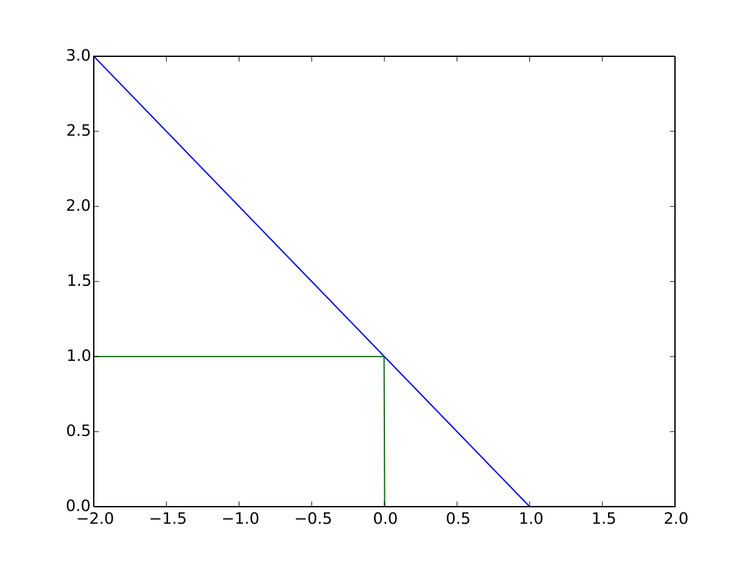
Hinge loss

Updated on
Edit
Like
Comment
Share on FacebookTweet on TwitterShare on LinkedInShare on Reddit
Hinge loss

In machine learning, the hinge loss is a loss function used for training classifiers. The hinge loss is used for "maximum-margin" classification, most notably for support vector machines (SVMs). For an intended output t = ±1 and a classifier score y, the hinge loss of the prediction y is defined as

Contents

ℓ ( y ) = max ( 0 , 1 − t ⋅ y )

Note that y should be the "raw" output of the classifier's decision function, not the predicted class label. For instance, in linear SVMs, y = w ⋅ x + b , where ( w , b ) are the parameters of the hyperplane and x is the point to classify.

It can be seen that when t and y have the same sign (meaning y predicts the right class) and | y | ≥ 1 , the hinge loss ℓ ( y ) = 0 , but when they have opposite sign, ℓ ( y ) increases linearly with y (one-sided error).

Extensions

While binary SVMs are commonly extended to multiclass classification in a one-vs.-all or one-vs.-one fashion, it is also possible to extend the hinge loss itself for such an end. Several different variations of multiclass hinge loss have been proposed. For example, Crammer and Singer defined it for a linear classifier as

ℓ ( y ) = max ( 0 , 1 + max t ≠ y w t x − w y x )

Weston and Watkins provided a similar definition, but with a sum rather than a max:

ℓ ( y ) = ∑ t ≠ y max ( 0 , 1 + w t x − w y x )

In structured prediction, the hinge loss can be further extended to structured output spaces. Structured SVMs with margin rescaling use the following variant, where y denotes the SVM's parameters, φ the joint feature function, and Δ the Hamming loss:

ℓ ( y ) = max ( 0 , Δ ( y , t ) + ⟨ w , ϕ ( x , y ) ⟩ − ⟨ w , ϕ ( x , t ) ⟩ ) = max ( 0 , max y ∈ Y ( Δ ( y , t ) + ⟨ w , ϕ ( x , y ) ⟩ ) − ⟨ w , ϕ ( x , t ) ⟩ )

Optimization

The hinge loss is a convex function, so many of the usual convex optimizers used in machine learning can work with it. It is not differentiable, but has a subgradient with respect to model parameters w of a linear SVM with score function y = w ⋅ x that is given by

∂ ℓ ∂ w i = { − t ⋅ x i if  t ⋅ y < 1 0 otherwise

However, since the derivative of the hinge loss at t y = 1 is non-deterministic, smoothed versions may be preferred for optimization, such as Rennie and Srebro's

ℓ ( y ) = { 1 2 − t y if     t y ≤ 0 , 1 2 ( 1 − t y ) 2 if     0 < t y ≤ 1 , 0 if     1 ≤ t y

or the quadratically smoothed

ℓ ( y ) = 1 2 γ max ( 0 , 1 − t y ) 2

suggested by Zhang. The modified Huber loss is a special case of this loss function with γ = 2 .

References

Hinge loss Wikipedia
(Text) CC BY-SA