Trisha Shetty (Editor)

Higman–Sims group

Updated on
Edit
Like
Comment
Share on FacebookTweet on TwitterShare on LinkedInShare on Reddit
Higman–Sims group

In the area of modern algebra known as group theory, the Higman–Sims group HS is a sporadic simple group of order

Contents

   29⋅32⋅53⋅7⋅11 = 44352000.

The Schur multiplier has order 2, the outer automorphism group has order 2, and the group 2.HS.2 appears as an involution centralizer in the Harada–Norton group.

History

HS is one of the 26 sporadic groups and was found by Donald G. Higman and Charles C. Sims (1968). They were attending a presentation by Marshall Hall on the Hall–Janko group J2. It happens that J2 acts as a permutation group on the Hall–Janko graph of 100 points, the stabilizer of one point being a subgroup with two other orbits of lengths 36 and 63. Inspired by this they decided to check for other rank 3 permutation groups on 100 points. They soon focused on a possible one containing the Mathieu group M22, which has permutation representations on 22 and 77 points. (The latter representation arises because the M22 Steiner system has 77 blocks.) By putting together these two representations, they found HS, with a one-point stabilizer isomorphic to M22.

HS is the simple subgroup of index two in the group of automorphisms of the Higman–Sims graph. The Higman–Sims graph has 100 nodes, so the Higman–Sims group HS is a transitive group of permutations of a 100 element set.

Graham Higman (1969) independently discovered the group as a doubly transitive permutation group acting on a certain 'geometry' on 176 points.

Relationship to Conway groups

Conway (1968) identified the Higman–Sims group as a subgroup of the Conway group Co0. In Co0 HS arises as a pointwise stabilizer of a 2-3-3 triangle, one whose edges (differences of vertices) are type 2 and 3 vectors. HS thus is a subgroup of each of the Conway groups Co0, Co2 and Co3.

In the Leech lattice, suppose a type 3 point v is fixed by an instance of Co3. Count the type 2 points w such that inner product v.w = 2 and thus v-w is type 3. Wilson (2009) (p. 208) shows their number is 11,178 = 2⋅35⋅23. He also shows this Co3 is transitive on these w. Hence the subgroup HS is well-defined.

|HS| = |Co3|/11,178 = 44,352,000.

In fact, | HS | = 100| M22 | and there are instances of HS including a permutation matrix representation of the Mathieu group M22.

If an instance of HS in Co0 fixes a particular point of type 3, this point is found in 276 triangles of type 2-2-3, which this copy of HS permutes in orbits of 176 and 100. This fact leads to Graham Higman's construction as well as to the Higman–Sims graph.

A 2-3-3 triangle defines a 2-dimensional subspace fixed pointwise by HS. The standard representation of HS can thus be reduced to a 22-dimensional one.

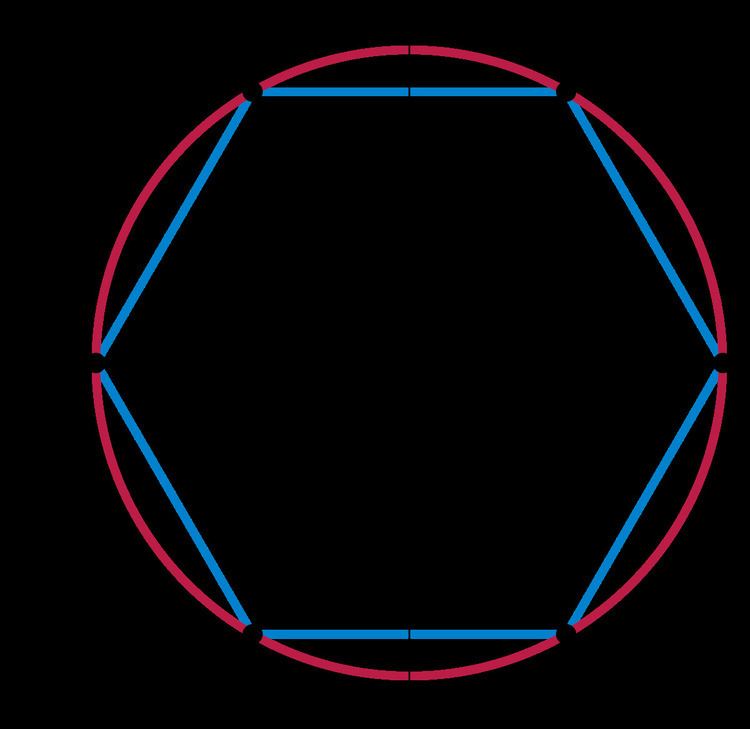
A Higman-Sims graph

Wilson (2009) (p. 210) gives an example of a Higman-Sims graph within the Leech lattice, permuted by the representation of M22 on the last 22 coordinates:

  • 22 points of shape (1, 1, −3, 121)
  • 77 points of shape (2, 2, 26, 016)
  • A 100th point (4, 4, 022)

    • Differences of adjacent points are of type 3; those of non-adjacent ones are of type 2.

    Here, HS fixes a 2-3-3 triangle with vertices x = (5, 123), y = (1, 5, 122), and z the origin. x and y are of type 3 while x-y = (4, −4, 022) is of type 2. Any vertex of the graph differs from x, y, and z by vectors of type 2.

    Two classes of involutions

    An involution in the subgroup M22 transposes 8 pairs of co-ordinates. As a permutation matrix in Co0 it has trace 8. It can shown that it moves 80 of the 100 vertices of the Higman-Sims graph. No transposed pair of vertices is an edge in the graph.

    There is another class of involutions, of trace 0, that move all 100 vertices. As permutations in the alternating group A100, being products of an odd number (25) of double transpositions, these involutions lift to elements of order 4 in the double cover 2.A100. HS thus has a double cover 2.HS.

    Maximal subgroups

    Magliveras (1971) found the 12 conjugacy classes of maximal subgroups of HS as follows:

  • M22, order 443520
  • U3(5):2, order 252000 – one-point stabilizer in doubly transitive representation of degree 176
  • U3(5):2 – conjugate to class above in HS:2
  • PSL(3,4):2, order 40320
  • S8, order 40320
  • 24.S6, order 11520
  • 43:PSL(3,2), order 10752
  • M11, order 7920
  • M11 – conjugate to class above in HS:2
  • 4.24.S5, order 7680 – centralizer of involution moving 80 vertices of Higman–Sims graph
  • 2 × A6.22, order 2880 – centralizer of involution moving all 100 vertices
  • 5:4 × A5, order 1200

    • Generalized Monstrous Moonshine

    Conway and Norton suggested in their 1979 paper that monstrous moonshine is not limited to the monster, but that similar phenomena may be found for other groups. Larissa Queen and others subsequently found that one can construct the expansions of many Hauptmoduln from simple combinations of dimensions of sporadic groups. For HS, the McKay-Thompson series is T 10 A ( τ ) where one can set a(0) = 4 ( A058097),

    j 10 A ( τ ) = T 10 A ( τ ) + 4 = ( ( η ( τ ) η ( 5 τ ) η ( 2 τ ) η ( 10 τ ) ) 2 + 2 2 ( η ( 2 τ ) η ( 10 τ ) η ( τ ) η ( 5 τ ) ) 2 ) 2 = ( ( η ( τ ) η ( 2 τ ) η ( 5 τ ) η ( 10 τ ) ) + 5 ( η ( 5 τ ) η ( 10 τ ) η ( τ ) η ( 2 τ ) ) ) 2 − 4 = 1 q + 4 + 22 q + 56 q 2 + 177 q 3 + 352 q 4 + 870 q 5 + 1584 q 6 + …

    References

    Higman–Sims group Wikipedia
    (Text) CC BY-SA