Puneet Varma (Editor)

Heterojunction

Updated on
Edit
Like
Comment
Share on FacebookTweet on TwitterShare on LinkedInShare on Reddit
Heterojunction

A heterojunction is the interface that occurs between two layers or regions of dissimilar crystalline semiconductors. These semiconducting materials have unequal band gaps as opposed to a homojunction. It is often advantageous to engineer the electronic energy bands in many solid-state device applications, including semiconductor lasers, solar cells and transistors ("heterotransistors") to name a few. The combination of multiple heterojunctions together in a device is called a heterostructure, although the two terms are commonly used interchangeably. The requirement that each material be a semiconductor with unequal band gaps is somewhat loose, especially on small length scales, where electronic properties depend on spatial properties. A more modern definition of heterojunction is the interface between any two solid-state materials, including crystalline and amorphous structures of metallic, insulating, fast ion conductor and semiconducting materials.

Contents

In 2000, the Nobel Prize in physics was awarded jointly to Herbert Kroemer (University of California, Santa Barbara, California, USA) and Zhores I. Alferov (Ioffe Institute, Saint Petersburg, Russia) for "developing semiconductor heterostructures used in high-speed- and opto-electronics".

Manufacture and applications

Heterojunction manufacturing generally requires the use of molecular beam epitaxy (MBE) or chemical vapor deposition (CVD) technologies in order to precisely control the deposition thickness and create a cleanly lattice-matched abrupt interface.

Despite their expense, heterojunctions have found use in a variety of specialized applications where their unique characteristics are critical:

  • Lasers: Using heterojunctions in lasers was first proposed in 1963 when Herbert Kroemer, a prominent scientist in this field, suggested that population inversion could be greatly enhanced by heterostructures. By incorporating a smaller direct band gap material like GaAs between two larger band gap layers like AlAs, carriers can be confined so that lasing can occur at room temperature with low threshold currents. It took many years for the material science of heterostructure fabrication to catch up with Kroemer's ideas but now it is the industry standard. It was later discovered that the band gap could be controlled by taking advantage of the quantum size effects in quantum well heterostructures. Furthermore, heterostructures can be used as waveguides to the index step which occurs at the interface, another major advantage to their use in semiconductor lasers. Semiconductor diode lasers used in CD and DVD players and fiber optic transceivers are manufactured using alternating layers of various III-V and II-VI compound semiconductors to form lasing heterostructures.
  • Bipolar transistors: When a heterojunction is used as the base-emitter junction of a bipolar junction transistor, extremely high forward gain and low reverse gain result. This translates into very good high frequency operation (values in tens to hundreds of GHz) and low leakage currents. This device is called a heterojunction bipolar transistor (HBT).
  • Field effect transistors: Heterojunctions are used in high electron mobility transistors (HEMT) which can operate at significantly higher frequencies (over 500 GHz). The proper doping profile and band alignment gives rise to extremely high electron mobilities by creating a two dimensional electron gas within a dopant free region where very little scattering can occur.

    • Energy band alignment

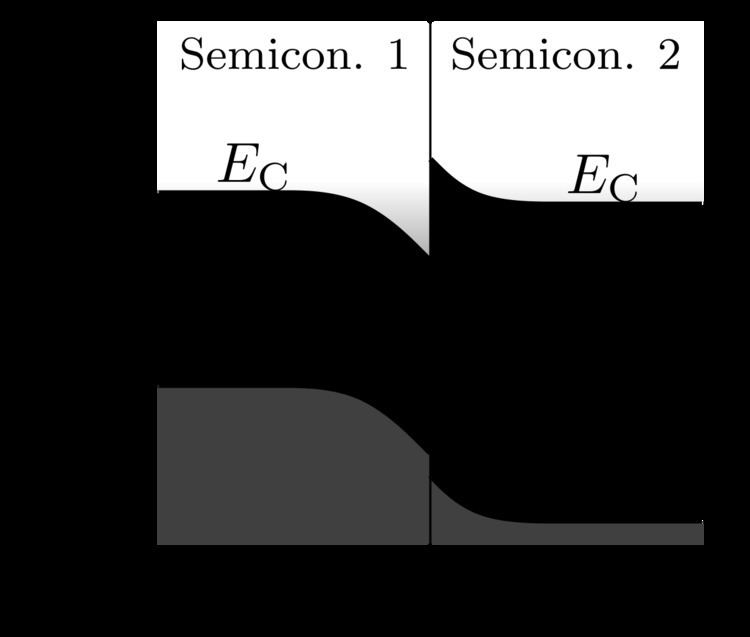
    The behaviour of a semiconductor junction depends crucially on the alignment of the energy bands at the interface. Semiconductor interfaces can be organized into three types of heterojunctions: straddling gap (type I), staggered gap (type II) or broken gap (type III) as seen in the figure. Away from the junction, the band bending can be computed based on the usual procedure of solving Poisson's equation.

    Various models exist to predict the band alignment.

  • The simplest (and least accurate) model is Anderson's rule, which predicts the band alignment based on the properties of vacuum-semiconductor interfaces (in particular the vacuum electron affinity). The main limitation is its neglect of chemical bonding.
  • A common anion rule was proposed which guesses that since the valence band is related to anionic states, materials with the same anions should have very small valence band offsets. This however did not explain the data but is related to the trend that two materials with different anions tend to have larger valence band offsets than conduction band offsets.
  • Tersoff proposed a gap state model based on more familiar metal-semiconductor junctions where the conduction band offset is given by the difference in Schottky barrier height. This model includes a dipole layer at the interface between the two semiconductors which arises from electron tunneling from the conduction band of one material into the gap of the other (analogous to metal-induced gap states). This model agrees well with systems where both materials are closely lattice matched such as GaAs/AlGaAs.
  • The 60:40 rule is a heuristic for the specific case of junctions between the semiconductor GaAs and the alloy semiconductor AlxGa1−xAs. As the x in the AlxGa1−xAs side is varied from 0 to 1, the ratio Δ E C / Δ E V tends to maintain the value 60/40. For comparison, Anderson's rule predicts Δ E C / Δ E V = 0.73 / 0.27 for a GaAs/AlAs junction (x=1).

    • The typical method for measuring band offsets is by calculating them from measuring exciton energies in the luminescence spectra.

    Effective mass mismatch at heterojunctions

    When a heterojunction is formed by two different semiconductors, a quantum well can be fabricated due to difference in band structure. In order to calculate the static energy levels within the achieved quantum well, understanding variation or mismatch of the effective mass across the heterojunction becomes substantial. The quantum well defined in the heterojunction can be treated as a finite well potential with width of l w . Addition to that, in 1966, Conley et al. and BenDaniel and Duke reported boundary condition for the envelope function in quantum well, known as BenDaniel-Duke boundary condition. According to them, the envelope function in fabricated quantum well must satisfy boundary condition which states ψ ( z ) , 1 m ∗ ∂ ∂ z ψ ( z ) are both continuous in interface regions.

    Nanoscale heterojunctions

    In quantum dots the band energies are dependent on crystal size due to the quantum size effects. This enables band offset engineering in nanoscale heterostructures. It is possible to use the same materials but change the type of junction, say from straddling (type I) to staggered (type II), by changing the size or thickness of the crystals involved. The most common nanoscale heterostructure system is ZnS on CdSe (CdSe@ZnS) which has a straddling gap (type I) offset. In this system the much larger band gap ZnS passivates the surface of the fluorescent CdSe core thereby increasing the quantum efficiency of the luminescence. There is an added bonus of increased thermal stability due to the stronger bonds in the ZnS shell as suggested by its larger band gap. Since CdSe and ZnS both grow in the zincblende crystal phase and are closely lattice matched, core shell growth is preferred. In other systems or under different growth conditions it may be possible to grow anisotropic structures such as the one seen in the image on the right.

    It has been shown that the driving force for charge transfer between conduction bands in these structures is the conduction band offset. By decreasing the size of CdSe nanocrystals grown on TiO2, Robel et al. found that electrons transferred faster from the higher CdSe conduction band into TiO2. In CdSe the quantum size effect is much more pronounced in the conduction band due to the smaller effective mass than in the valence band, and this is the case with most semiconductors. Consequently, engineering the conduction band offset is typically much easier with nanoscale heterojunctions. For staggered (type II) offset nanoscale heterojunctions, photoinduced charge separation can occur since there the lowest energy state for holes may be on one side of the junction whereas the lowest energy for electrons is on the opposite side. It has been suggested that anisotropic staggered gap (type II) nanoscale heterojunctions may be used for photocatalysis, specifically for water splitting with solar energy.

    References

    Heterojunction Wikipedia
    (Text) CC BY-SA