Appearance Colourless gas | ||
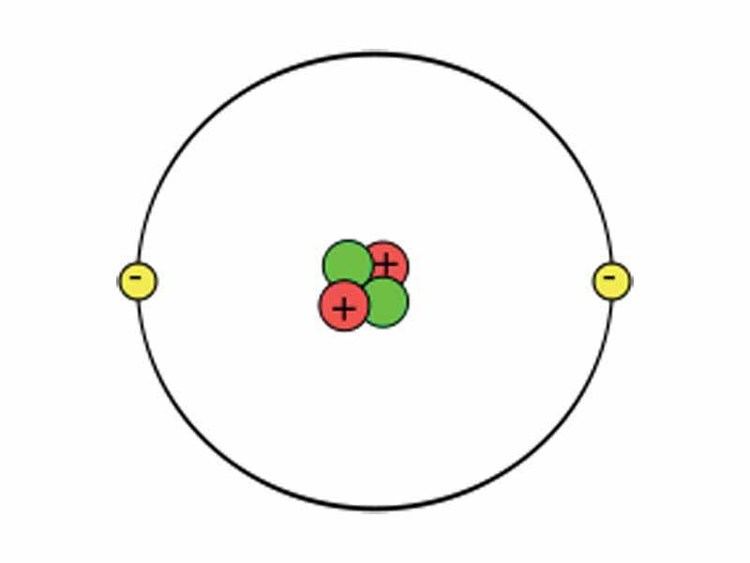 | ||
Lewis dot structure for helium atom he
A helium atom is an atom of the chemical element helium. Helium is composed of two electrons bound by the electromagnetic force to a nucleus containing two protons along with either one or two neutrons, depending on the isotope, held together by the strong force. Unlike for hydrogen, a closed-form solution to the Schrödinger equation for the helium atom has not been found. However, various approximations, such as the Hartree–Fock method, can be used to estimate the ground state energy and wavefunction of the atom.
Contents
- Lewis dot structure for helium atom he
- Helium atom 3d animation loop
- Introduction
- HartreeFock method
- ThomasFermi method
- The variational method
- Experimental value of ionization energy
- References
Helium atom 3d animation loop
Introduction
The quantum mechanical description of the helium atom is of special interest, because it is the simplest multi-electron system and can be used to understand the concept of quantum entanglement. The Hamiltonian of helium, considered as a three-body system of two electrons and a nucleus and after separating out the centre-of-mass motion, can be written as
where
It is important to note, that it operates not in normal space, but in a 6-dimensionsional configuration space
It is easy to show, that the singlet state is invariant under all rotations (a scalar entity), while the triplet can be mapped to an ordinary space vector. Since all spin interaction terms between the four components of
The spin here only comes into play through the Pauli exclusion principle, which for fermions (like electrons) requires antisymmetry under simultaneous exchange of spin and coordinates
Parahelium is then the singlet state
This explains the absence of the
If the electron-electron interaction term
Nevertheless, quite good theoretical descriptions of helium can be obtained within the Hartree–Fock and Thomas–Fermi approximations (see below).
Hartree–Fock method
The Hartree–Fock method is used for a variety of atomic systems. However it is just an approximation, and there are more accurate and efficient methods used today to solve atomic systems. The "many-body problem" for helium and other few electron systems can be solved quite accurately. For example the ground state of helium is known to fifteen digits. In Hartree–Fock theory, the electrons are assumed to move in a potential created by the nucleus and the other electrons. The Hamiltonian for helium with two electrons can be written as a sum of the Hamiltonians for each electron:
where the zero-order unperturbed Hamiltonian is
while the perturbation term:
is the electron-electron interaction. H0 is just the sum of the two hydrogenic Hamiltonians:
where
Eni, the energy eigenvalues and
where
Neglecting the electron-electron repulsion term, the Schrödinger equation for the spatial part of the two-electron wave function will reduce to the 'zero-order' equation
This equation is separable and the eigenfunctions can be written in the form of single products of hydrogenic wave functions:
The corresponding energies are (in atomic units, hereafter a.u.):
Note that the wave function
An exchange of electron labels corresponds to the same energy
This comes from Slater determinants.
The factor
Where
where E
The energy that we obtained is too low because the repulsion term between the electrons was ignored, whose effect is to raise the energy levels. As Z gets bigger, our approach should yield better results, since the electron-electron repulsion term will get smaller.
So far a very crude independent-particle approximation has been used, in which the electron-electron repulsion term is completely omitted. Splitting the Hamiltonian showed below will improve the results:
where
and
V(r) is a central potential which is chosen so that the effect of the perturbation
where S is a screening constant and the quantity Ze is the effective charge. The potential is a Coulomb interaction, so the corresponding individual electron energies are given (in a.u.) by
and the corresponding wave function is given by
If Ze was 1.70, that would make the expression above for the ground state energy agree with the experimental value E0 = -2.903 a.u. of the ground state energy of helium. Since Z = 2 in this case, the screening constant is S = .30. For the ground state of helium, for the average shielding approximation, the screening effect of each electron on the other one is equivalent to about
Thomas–Fermi method
Not long after Schrödinger developed the wave equation, the Thomas–Fermi model was developed. Density functional theory is used to describe the particle density
The energy functional for an atom with N electrons is given by:
Where
The electron density needs to be greater than or equal to 0,
In the energy functional, each term holds a certain meaning. The first term describes the minimum quantum-mechanical kinetic energy required to create the electron density
So the Hamiltonian for a system of many electrons can be written:
For helium, N = 2, so the Hamiltonian is given by:
Where
yielding
From the Hartree–Fock method, it is known that ignoring the electron-electron repulsion term, the energy is 8E1 = -109 eV.
The variational method
To obtain a more accurate energy the variational principle can be applied to the electron-electron potential Vee using the wave function
After integrating this, the result is:
This is closer to the theoretical value, but if a better trial wave function is used, an even more accurate answer could be obtained. An ideal wave function would be one that doesn't ignore the influence of the other electron. In other words, each electron represents a cloud of negative charge which somewhat shields the nucleus so that the other electron actually sees an effective nuclear charge Z that is less than 2. A wave function of this type is given by:
Treating Z as a variational parameter to minimize H. The Hamiltonian using the wave function above is given by:
After calculating the expectation value of
The minimum value of Z needs to be calculated, so taking a derivative with respect to Z and setting the equation to 0 will give the minimum value of Z:
This shows that the other electron somewhat shields the nucleus reducing the effective charge from 2 to 1.69. So we obtain the most accurate result yet:
Where again, E1 represents the ionization energy of hydrogen.
By contrast, we can also use the formula to obtain the best result:
Where
By using more complicated/accurate wave functions, the ground state energy of helium has been calculated closer and closer to the experimental value -78.95 eV. The variational approach has been refined to very high accuracy for a comprehensive regime of quantum states by G.W.F. Drake and co-workers as well as J.D. Morgan III, Jonathan Baker and Robert Hill using Hylleraas or Frankowski-Pekeris basis functions. It should be noted that one needs to include relativistic and quantum electrodynamic corrections to get full agreement with experiment to spectroscopic accuracy.
Experimental value of ionization energy
Helium's first ionization energy is -24.587387936(25)eV. This value was derived by experiment. The theoretic value of Helium atom's second ionization energy is -54.41776311(2)eV. The total ground state energy of the helium atom is -79.005151042(40)eV, or -2.90338583(13)a.u.
