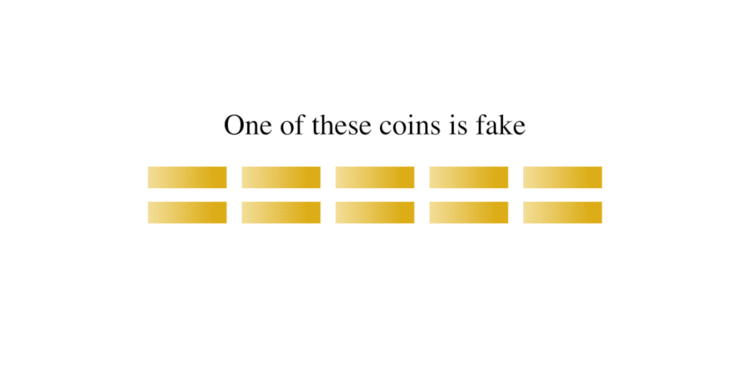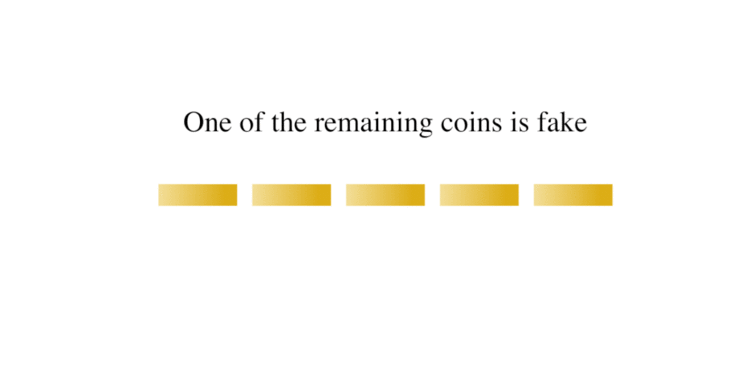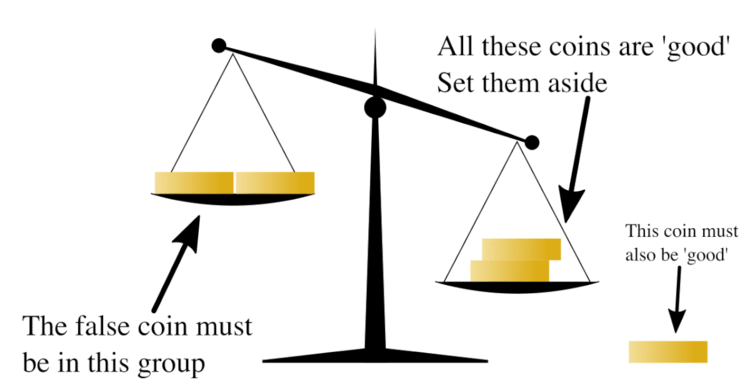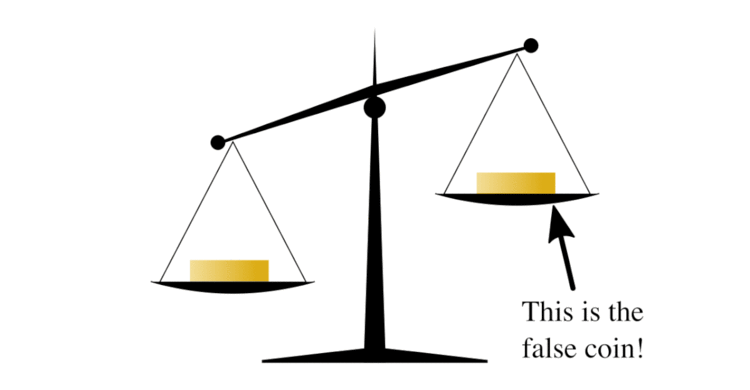Group testing

Background

The field of (Combinatorial) Group Testing was introduced by Robert Dorfman in 1943. The motivation arose during the Second World War when the United States Public Health Service and the Selective service embarked upon a large scale project to weed out all syphilitic men called up for induction. Testing an individual for syphilis involves drawing a blood sample from them and then analysing the sample to determine the presence or absence of syphilis. However, at the time, performing this test was expensive, and testing every soldier individually would have been very cost heavy and inefficient.

Supposing there are n soldiers, this method of testing leads to n separate tests. If we have 70-75% of the people infected then this method would be reasonable. Our goal however, is to achieve effective testing in the more likely scenario where it does not make sense to test 100,000 people to get (say) 10 positives.

The feasibility of a more effective testing scheme hinges on the following property. We can combine blood samples and test a combined sample together to check if at least one soldier has syphilis. This is the central idea behind group testing. If one or more of the soldiers in this group has syphilis, then a test is wasted (more tests need to be performed to find which soldier(s) it was). On the other hand, if no one in the pool has syphilis then many tests are saved.

Modern interest in these testing schemes has been rekindled by the Human Genome Project.

Types of group-testing algorithm

Group-testing algorithms can be described as adaptive or non-adaptive. An adaptive algorithm proceeds by performing a test, and then using the result (and all past results) to decide which next test to perform. On the other hand, in non-adaptive algorithms all tests are decided in advance. Although adaptive algorithms offer much more freedom in design, it is known that adaptive group-testing algorithms do not improve upon non-adaptive group-testing algorithms by more than a constant factor in the number of tests required to identify the set of defective items. In addition to this, non-adaptive methods are often useful in practice because one knows in advance all the tests one needs to perform, allowing for the effective distribution of the testing process.

As well as adaptivity, all group testing algorithms are either combinatorial or probabilistic. A combinatorial algorithm finds all the defectives with certainty. In contrast, a probabilistic algorithm has some non-zero probability of making a mistake (i.e. deciding a defective item is non-defective or vice versa). It is known that zero-error algorithms require significantly more tests asymptotically (in the number of defective items) than algorithms that allow asymptotically small probabilities of error.

Another class of algorithms are so-called noisy algorithms. These deal with the situation that with some non-zero probability, q , the result of a group test is erroneous (e.g. comes out positive when the test contained no defectives). A noisy algorithm will always have a non-zero probability of making a mistake.

Formalization of the problem

We now formalize the group-testing problem abstractly.

Let the total number of items to be tested be n , and an upper bound on the number of defective items be d . The (unknown) information about which items are defective is described as a vector, x = ( x 1 , x 2 , . . . , x n ) , where x i = 1 if i-th item is defective and x i = 0 otherwise. x is called the input vector.

The Hamming Weight of x is defined as the number of 1 's in x . Hence, | x | ≤ d where | x | is the Hamming weight. The vector x is an implicit input since we do not know the positions of the 1 's. The only way to find out is to run the tests.

Formal notion of a test

A query/test S is a subset of [ n ] . The answer to the query S ⊆ [ n ] is defined as follows:

A ( S ) = { 1 ,  if  ∑ k ∈ S x k ≥ 1 0 ,  otherwise.

Note that the addition operation used by the summation is the logical OR, i.e.

A ( S ) = ⋁ i ∈ S x i .

Goal

The goal of group testing is to compute or estimate x and minimize the number of tests required to do so. Here, we have no direct questions or answers. Any piece of information can only be obtained using an indirect query. Group testing is ultimately a question of combinatorial searching. The major issue with such problems is that the solution can grow exponentially in the size of the input.

Definitions and initial bounds

t ( d , n ) is defined as the minimum number of non-adaptive tests that one would have to make to detect all of d defective items with a total of n items. Similarly, we use t a ( d , n ) to denote the number of adaptive tests that one would have to make to detect all the defective items.

Consider the case when only one person in the group will test positive. Then if we tested in the naive way, in the best case we would at least have to test the first person to find out if he/she is infected. However, in the worst case one might have to end up testing the entire group and only the last person we test will turn out to really be the one who was infected. Hence, 1 ≤ t ( d , n ) ≤ n . We also have that t a ( d , n ) ≤ t ( d , n ) due to the fact that any non-adaptive test can be performed by an adaptive test by running all of the tests in the first step of the adaptive test. Adaptive tests can be more efficient than non-adaptive tests since the test can be changed after certain things are discovered.

In summary, 1 ≤ t a ( d , n ) ≤ t ( d , n ) ≤ n .

Mathematical representation of non-adaptive algorithms

Algorithms for non-adaptive group testing consist of two distinct phases. First, it is decided how many tests to perform and which items to include in each test. This is usually encoded in an t × n binary matrix, M , where t is the number of tests and n is the total number of items. Each column of M represents an item and each row represents a test, with a 1 in the (i,j)^th entry indicating that the i-th test included the j-th item and a 0 indicating otherwise. In the second phase, often called the decoding step, the results of each group test are analysed to determine which items are likely to be defective.

As well as the vector x (of length n ) that describes the (unknown) defective set, we introduce the vector y , of length t , describing the results of each test. A 1 in the j-th entry of y indicates that the j-th test was positive (i.e. contained at least one defective). With these vectors the problem can be reframed as follows: first we choose some testing matrix, M , after which we are given y . Then the problem is to analyse y to find some estimate for x .

These notions can be expressed more formally as follows. Let S ⊆ [ n ] be a test and define χ i ∈ { 0 , 1 } n such that i ∈ S ⇔ χ s ( i ) = 1 , so the k-th test is described by χ k . Let M be the t × n matrix with rows χ i , so that ( M ) i , j = χ i ( j ) . This construction is based on the grounds that non-adaptive testing with t tests is represented by a t -subset S i ⊆ [ n ] where 1 ≤ i ≤ t .

Under this setup, y is defined by the matrix multiplication relation: M x = y , where multiplication is logical AND ( ∧ ) and addition is logical OR ( ∨ ). Here, y will have a 1 in position i if and only if ( M ) i , j and x j are both 1 for any j . That is, if and only if at least one defective item was included in the i-th test.

Generalized binary splitting algorithm

The generalized binary splitting algorithm is an essentially-optimal adaptive group-testing algorithm that proceeds as follows:

1. If n ≤ 2 d − 2 , test the n items individually. Otherwise, set l = n − d + 1 and α = ⌊ log ⁡ l / d ⌋ .
2. Test a group of size 2 α . If the outcome is negative, every item in the group is declared to be non-defective; set n := n − 2 α and go to step 1. Otherwise, use a binary search to identify one defective and an unspecified number, called x , of non-defective items; set n := n − 1 − x and d := d − 1 . Go to step 1.

The generalized binary splitting algorithm requires no more than T tests where T = { n n ≤ 2 d − 2 ( α + 2 ) d + p − 1 n ≥ 2 d − 1 .

Non-adaptive algorithms

Non-adaptive group-testing algorithms tend to assume that the number of defectives, or at least a good upper bound on them, is known. We will denote this quantity d . If no bounds are known, there are non-adaptive algorithms with low query complexity that can help estimate d .

Combinatorial Orthogonal Matching Pursuit (COMP)

Combinatorial Orthogonal Matching Pursuit, or COMP, is a simple non-adaptive group-testing algorithm that forms the basis for the more complicated algorithms that follow in this section.

First, each entry of the testing matrix is chosen i.i.d. to be 1 with probability 1 / d and 0 otherwise.

The decoding step proceeds column-wise (i.e. by item). If every test in which an item appears is positive, then the item is declared defective; otherwise the item is assumed to be non-defective. Or equivalently, if an item appears in any test whose outcome is negative, the item is declared non-defective; otherwise the item is assumed to be defective. Of particular note here is that this algorithm never creates false negatives, though a false positive occurs when all locations with ones in the j-th column of M (corresponding to a non-defective item j) are “hidden” by the ones of other columns corresponding to defective items.

The COMP algorithm requires no more than e d ( 1 + δ ) ln ⁡ ( n ) tests to have an error probability less than or equal to n − δ .

In the noisy case, we relax the requirement in the original COMP algorithm that the set of locations of ones in any column of M corresponding to a positive item be entirely contained in the set of locations of ones in the result vector. Instead, we allow for a certain number of “mismatches” – this number of mismatches depends on both the number of ones in each column, and also the noise parameter, q . This noisy COMP algorithm requires no requires no more than 4.36 ( δ + 1 + δ ) 2 ( 1 − 2 q ) − 2 d log ⁡ n tests to achieve an error probability at most n − δ .

Definite Defectives (DD)

The definite defectives method is an extension of the COMP algorithm that attempts to remove any false positives. Performance guarantees for DD have been shown to strictly exceed those of COMP.

The decoding step uses a useful property of the COMP algorithm: that every item that COMP declares non-defective is certainly non-defective (that is, there are no false negatives). It proceeds as follows:

1. We first run the COMP algorithm, and remove any non-defectives that it detects. All remaining items are now “possibly defective”
2. Next the algorithm looks at all the positive tests. If an item appears as the only “possible defective” in a test, then it must be defective, so the algorithm declares it to be defective.
3. All other items are assumed to be non-defective. The justification for this last step comes from the assumption that the number of defectives is much smaller than the total number of items.

Note that steps 1 and 2 never make a mistake, so the algorithm can only make a mistake if it declares a defective item to be non-defective. Thus the DD algorithm can only create false negatives.

Sequential COMP (SCOMP)

SCOMP is an algorithm that makes use of the fact that DD makes no mistakes until the last step, were we assume remaining items to be defective. Let the set of declared defectives be K . We say that a positive test is explained by K if it contains at least one item in K . The key observation with SCOMP is that the set of defectives found by DD may not explain every positive test, and that every unexplained test must contain a hidden defective.

The algorithm proceeds as follows:

1. First carry out steps 1 and 2 of the DD algorithm to obtain K , an initial estimate for the set of defectives.
2. If K explains every positive test, terminate the algorithm: K is our final estimate for the set of defectives.
3. If there are any unexplained tests, find the “possible defective” that appears in the largest number of unexplained tests, and declare it to be defective (that is, add it to the set K ). Go to step 2.

In simulations, SCOMP has been shown to perform close to optimally.

Bounds

In the combinatorial setup, there are a number of upper and lower bounds on t(d,n) (and t^a(d,n)), the minimum number of tests required to detect all defectives.

Lower bound on t a ( d , n ) {displaystyle t^{a}(d,n)}

Fix a valid group testing scheme with t tests. Now, for two distinct input vectors x and x ′ where | x | , | x ′ | ≤ d , the resulting vectors will not be the same i.e. y ( x ) ≠ y ( x ′ ) , were y ( x ) is the resultant for input vector x . This is because two valid inputs will never give us the same result. If this ever happened, then we would always have an error in finding both x and x ′ . This gives us that the total number of distinct results is the volume of a Hamming Ball of radius d , centered about n i.e. V o l 2 ( d , n ) . However, for t bits, the total number of possible distinct vectors is 2 t . Hence, 2 t ≥ V o l 2 ( d , n ) . Taking the log on both sides gives us t ≥ log ⁡ { V o l 2 ( d , n ) } .

Now, V o l 2 ( d , n ) ≥ ( n d ) ≥ ( n d ) d . Therefore, we will end up having to perform a minimum of d log ⁡ n d tests.

Thus we have proved that t a ( d , n ) ≥ d log ⁡ n d

Upper bound on t a ( d , n ) {displaystyle t^{a}(d,n)}

t a ( d , n ) ≤ O ( d log ⁡ n ) .

Since we know that the upper bound on the number of positives is d , we run a binary search at most d times or until there are no more values to be found. To simplify the problem we try to give a testing scheme that uses O ( log ⁡ n ) adaptive tests to figure out a i such that x i = 1 . The related problem is solved by splitting [ n ] in two halves and querying to find a 1 in one of those and then proceeding recursively to find the exact position in the half where the query returned a 1 . This will take 2 ⌈ log ⁡ n ⌉ time or if the first query is performed on the whole set, it will take ⌈ log ⁡ n ⌉ + 1 . Once a 1 is found, the search is then repeated after removing the i t h co-ordinate. This can be done at most d times. This justifies the running time of O ( d log ⁡ n ) . For a full proof and an algorithm for the problem refer to: CSE545 at the University at Buffalo

Upper bound on t ( 1 , n ) {displaystyle t(1,n)}

t ( 1 , n ) ≤ ⌈ log ⁡ n ⌉ This upper bound is for the special case where d = 1 i.e. there is a maximum of 1 positive. In this case, the matrix multiplication gets simplified and the resultant y represents the binary representation of i for test i . This gives a lower bound of ⌈ log ⁡ n ⌉ . Note that decoding becomes trivial because the binary representation of i gives us the location directly. The group test matrix here is just the parity check matrix H m for the [ 2 m − 1 , 2 m − m − 1 , 3 ] Hamming code.

Thus as the upper and lower bounds are the same, we have a tight bound for t ( d , n ) when d = 1 . Such tight bounds are not known for general d .

Upper bounds for non-adaptive group testing

For non-adaptive group testing upper bounds we shift focus toward disjunct matrices, which have been used for many of the bounds because of their nice properties. It has been shown that Ω ( d 2 log ⁡ d log ⁡ n ) ≤ t ( d , n ) . Also for upper bounds we currently have t ( d , n ) ≤ O ( d 2 log ⁡ n ) with a strongly explicit construction. So the smallest upper bound and biggest lower bound they are only off by a factor of 1 / log ⁡ d , which is fairly small.

Separately, we can see that the current known lower bound for t ( d , n ) is already a factor of d / log ⁡ d larger than the upper bound for t a ( d , n ) .