Generalized helicoid

Screw motion of a point

Moving a point on a screwtype curve means, the point is rotated and displaced along a line (axis) such that the displacement is proportional to the rotation-angle. The result is a circular helix.

If the axis is the z-axis, the motion of a point P 0 = ( x 0 , y 0 , z 0 ) can be described parametrically by

p ( φ ) = ( x 0 cos ⁡ φ − y 0 sin ⁡ φ x 0 sin ⁡ φ + y 0 cos ⁡ φ z 0 + c φ )   ,   φ ∈ R   .

c ≠ 0 is called slant, the angle φ , measured in radian, is called the screw angle and h = c 2 π the pitch (green). The trace of the point is a circular helix (red). It is contained in the surface of a right circular cylinder. Its radius is the distance of point P 0 to the z-axis.

In case of c > 0 , the helix is called right handed otherwise left handed. (In case of c = 0 the motion is a rotation around the z-axis).

Screw motion of a curve

The screw motion of curve

x ( t ) = ( x ( t ) , y ( t ) , z ( t ) ) T ,   t 1 ≤ t ≤ t 2   ,

yields a generalized helicoid with the parametric representation

S ( t , φ ) = ( x ( t ) cos ⁡ φ − y ( t ) sin ⁡ φ x ( t ) sin ⁡ φ + y ( t ) cos ⁡ φ z ( t ) + c φ )   , t 1 ≤ t ≤ t 2 ,   φ ∈ R   .

The curves S ( t = constant , φ ) are circular helices.
The curves S ( t , φ = constant ) are copies of the given profile curve.

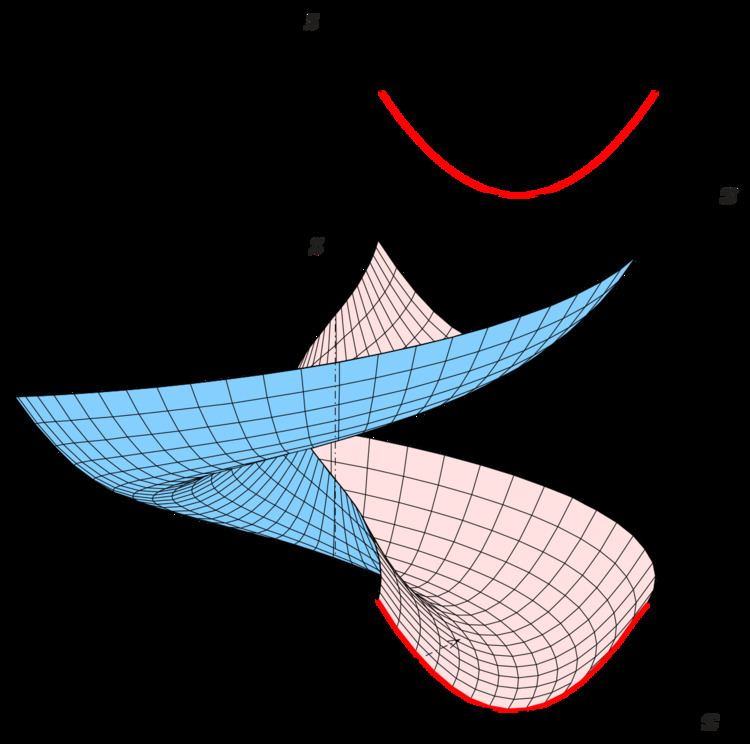
Example: For the first picture above, the meridian is a parabola.

Types

If the profile curve is a line one gets a ruled generalized helicoid. There are four types:

(1) The line intersects the axis orthogonally. One gets a helicoid (closed right ruled generalized helicoid).(2) The line intersects the axis, but not orthogonally. One gets an oblique closed type.

If the given line and the axis are skew lines one gets an open type and the axis is not part of the surface (s. picture).

(3) If the given line and the axis are skew lines and the line is contained in a plane orthogonally to the axis one gets a right open type or shortly open helicoid.(4) If the line and the axis are skew and the line is not contained in ... (s. 3) one gets an oblique open type.

Oblique types do intersect themselves (s. picture), right types (helicoids) do not.

One gets an interesting case, if the line is skew to the axis and the product of its distance d to the axis and its slope is exactly c . In this case the surface is a tangent developable surface and is generated by the directrix ( d cos ⁡ φ , d sin ⁡ φ , c φ ) .

Remark:

1. The (open and closed) helicoids are Catalan surfaces. The closed type (common helicoid) is even a conoid
2. Ruled generalized helicoids are not algebraic surfaces.

On closed ruled generalized helicoids

A closed ruled generalized helicoid has a profile line that intersects the axis. If the profile line is described by ( t , 0 , z 0 + m t ) T one gets the following parametric representation

S ( t , φ ) = ( t cos ⁡ φ t sin ⁡ φ z 0 + m t + c φ )   .

If m = 0 (common helicoid) the surface does not intersect itself.
If m ≠ 0 (oblique type) the surface intersects itself and the curves (on the surface)

S ( t i , φ ) with t i = h 4 m ( 2 i + 1 ) ,   i = 1 , 2 , …

consist of double points. There exist infinite double curves. The smaller | m | the greater are the distances between the double curves.

On the tangent developable type

For the directrix (a helix)

x ( φ ) = ( r cos ⁡ φ , r sin ⁡ φ , c φ ) T

one gets the following parametric representation of the tangent developable surface:

S ( t , φ ) = x ( φ ) + t x ˙ ( φ ) = ( r cos ⁡ φ − t r sin ⁡ φ r sin ⁡ φ + t r cos ⁡ φ c ( t + φ ) )   .

The surface normal vector is

n = S t × S φ = x ˙ × ( x ˙ + t x ¨ ) = t ( x ˙ × x ¨ ) = t ( c r sin ⁡ φ − c r cos ⁡ φ r 2 )   .

For t = 0 the normal vector is the null vector. Hence the directrix consists of singular points. The directrix separates two regular parts of the surface (s. picture).

Circular generalized helicoids

There are 3 interesting types of circular generalized helicoids:

(1) If the circle is a meridian and does not intersect the axis (s. picture).(2) The plane that contains the circle is orthogonal to the helix of the circle centers. One gets a pipe surface(3) The circle's plane is orthogonal to the axis and comprises the axis point in it (s. picture). This type was used for baroque-columns.