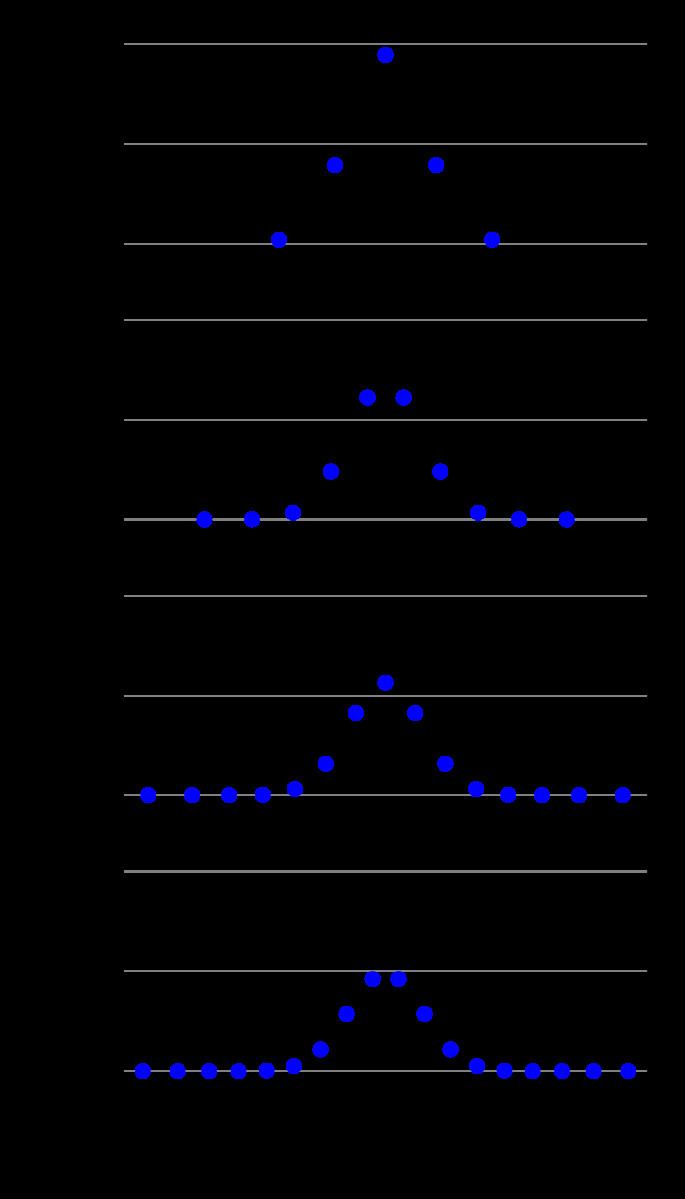
Gauss–Hermite quadrature - Alchetron, the free social encyclopedia

In numerical analysis, Gauss–Hermite quadrature is a form of Gaussian quadrature for approximating the value of integrals of the following kind:

∫ − ∞ + ∞ e − x 2 f ( x ) d x .

In this case

∫ − ∞ + ∞ e − x 2 f ( x ) d x ≈ ∑ i = 1 n w i f ( x i )

where n is the number of sample points used. The x_i are the roots of the physicists' version of the Hermite polynomial H_n(x) (i = 1,2,...,n), and the associated weights w_i are given by

w i = 2 n − 1 n ! π n 2 [ H n − 1 ( x i ) ] 2 .

Example with change of variable

Let's consider a function h(y), where the variable y is Normally distributed: y ∼ N ( μ , σ 2 ) . The expectation of h corresponds to the following integral:

E [ h ( y ) ] = ∫ − ∞ + ∞ 1 σ 2 π exp ⁡ ( − ( y − μ ) 2 2 σ 2 ) h ( y ) d y

As this doesn't exactly correspond to the Hermite polynomial, we need to change variables:

x = y − μ 2 σ ⇔ y = 2 σ x + μ

Coupled with the integration by substitution, we obtain:

E [ h ( y ) ] = ∫ − ∞ + ∞ 1 π exp ⁡ ( − x 2 ) h ( 2 σ x + μ ) d x

leading to:

E [ h ( y ) ] ≈ 1 π ∑ i = 1 n w i h ( 2 σ x i + μ )

References

Gauss–Hermite quadrature Wikipedia

(Text) CC BY-SA