In mathematics, a functional square root (sometimes called a half iterate) is a square root of a function with respect to the operation of function composition. In other words, a functional square root of a function g is a function f satisfying f(f(x)) = g(x) for all x.
Notations expressing that f is a functional square root of g are f = g[1/2] and f = g1/2.
The functional square root of the exponential function (now known as a half-exponential function) was studied by Hellmuth Kneser in 1950.The solutions of f(f(x)) = x over R (the involutions of the real numbers) were first studied by Charles Babbage in 1815, and this equation is called Babbage's functional equation. A particular solution is f(x) = (b − x)/(1 + cx) for bc ≠ −1. Babbage noted that for any given solution f, its functional conjugate Ψ−1 ○ f ○ Ψ by an arbitrary invertible function Ψ is also a solution.A systematic procedure to produce arbitrary functional n-roots (including, beyond n = 1/2, continuous, negative, and infinitesimal n) relies on the solutions of Schröder's equation.
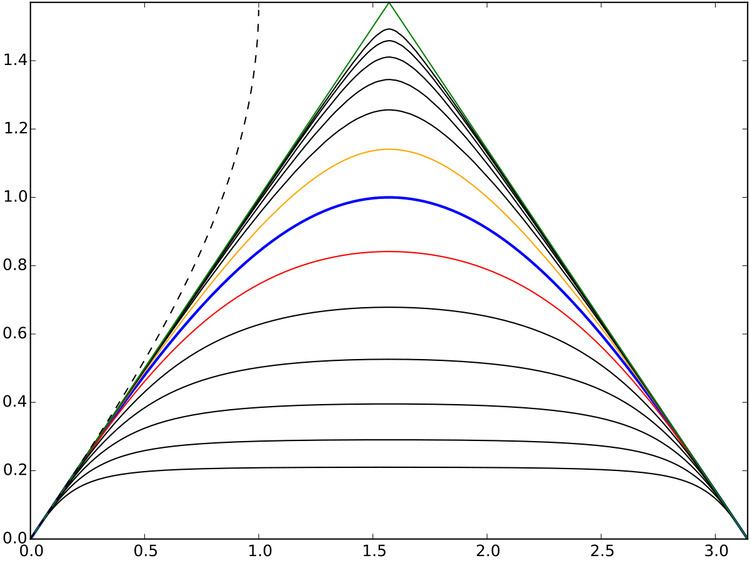
f(x) = 2x2 is a functional square root of g(x) = 8x4.A functional square root of the nth Chebyshev polynomial, g(x) = Tn(x), is f(x) = cos(√n arccos(x)), which in general is not a polynomial.f(x) = x/(√2 + x(1 − √2)) is a functional square root of g(x) = x/(2 − x).sin[2](x) = sin(sin(x)) [
red curve]
sin[1](x) = sin(x) = rin(rin(x)) [
blue curve]
sin[½](x) = rin(x) = qin(qin(x)) [
orange curve]
sin[¼](x) = qin(x) [black curve above the orange curve]
sin[–1](x) = arcsin(x) [dashed curve]
(Cf. the general pedagogy web-site. For the notation, see [1].)