 | ||
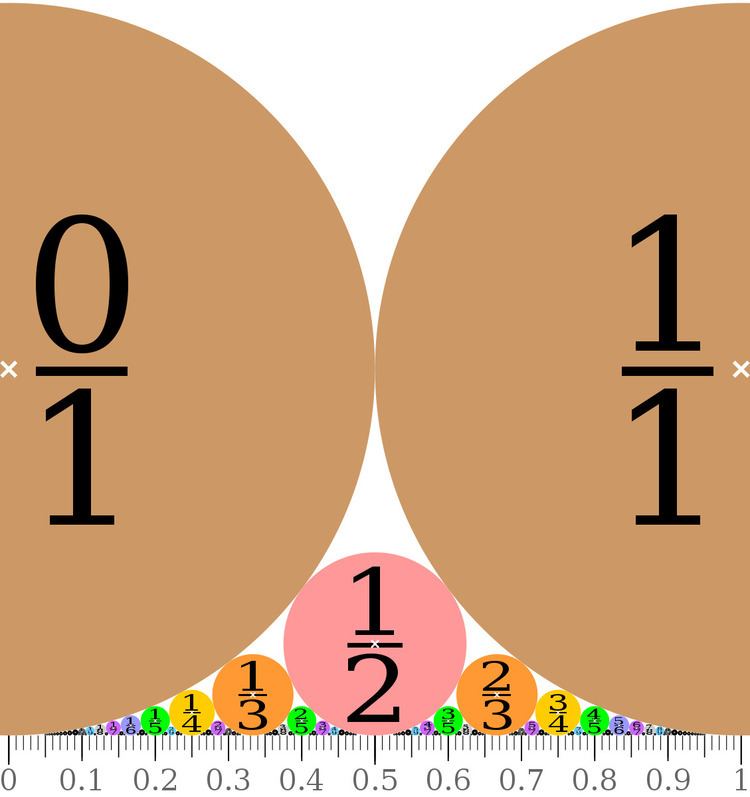
In mathematics, a Ford circle is a circle with center at
Contents
History
Ford circles are a special case of mutually tangent circles; the base line can be thought of as a circle with infinite radius. Systems of mutually tangent circles were studied by Apollonius of Perga, after whom the problem of Apollonius and the Apollonian gasket are named. In the 17th century René Descartes discovered Descartes' theorem, a relationship between the reciprocals of the radii of mutually tangent circles.
Ford circles also appear in the Sangaku (geometrical puzzles) of Japanese mathematics. A typical problem, which is presented on an 1824 tablet in the Gunma Prefecture, covers the relationship of three touching circles with a common tangent. Given the size of the two outer large circles, what is the size of the small circle between them? The answer is equivalent to a Ford circle:
Ford circles are named after the American mathematician Lester R. Ford, Sr., who wrote about them in 1938.
Properties
The Ford circle associated with the fraction
Two different Ford circles are either disjoint or tangent to one another. No two interiors of Ford circles intersect, even though there is a Ford circle tangent to the x-axis at each point on it with rational coordinates. If
- the circles
C [ r / s ] where| p s − q r | = 1 , - the circles associated with the fractions
r / s that are the neighbors ofp / q in some Farey sequence, or - the circles
C [ r / s ] wherer / s is the next larger or the next smaller ancestor top / q in the Stern–Brocot tree or wherep / q is the next larger or next smaller ancestor tor / s .
If
Ford circles can also be thought of as curves in the complex plane. The modular group of transformations of the complex plane maps Ford circles to other Ford circles.
Ford circles are a sub-set of the circles in the Apollonian gasket generated by the lines
By interpreting the upper half of the complex plane as a model of the hyperbolic plane (the Poincaré half-plane model) Ford circles can be interpreted as horocycles. In hyperbolic geometry any two horocycles are congruent . When these horocycles are circumscribed by apeirogons they tile the hyperbolic plane with an order-3 apeirogonal tiling.
Total area of Ford circles
There is a link between the area of Ford circles, Euler's totient function
is less than 1. In fact the total area of these Ford circles is given by a convergent sum, which can be evaluated. From the definition, the area is
Simplifying this expression gives
where the last equality reflects the Dirichlet generating function for Euler's totient function
