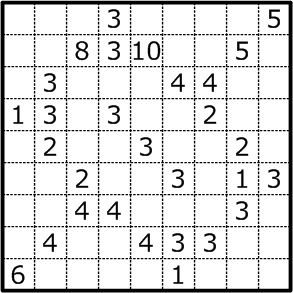
 | ||
Fillomino (フィルオミノ) is a type of logic puzzle published by many publishers. Other published titles for the puzzle include Allied Occupation.
Contents
Rules
Fillomino is played on a rectangular grid with no standard size; the internal grid lines are often dotted. (When published as Allied Occupation in the World Puzzle Championship, the cells of the grid are circular, but this is purely an aesthetic concern.) Some cells of the grid start containing numbers, referred to as "givens". The goal is to divide the grid into polyominoes (by filling in their boundaries) such that each given number n in the grid is part of an n-omino and that no two polyominoes of matching size (number of cells) are orthogonally adjacent (share a side).
Unlike some of its contemporaries among puzzles, there need not be a one-to-one correspondence between givens and polyominoes in the solution; it is possible for two givens with matching number to belong to the same polyomino in the solution, and for a polyomino to have no given at all.
Solution methods
It is common practice in solving a Fillomino puzzle to add numbers to the empty cells when it is determined what size polyomino each must belong to; these numbers are effectively treated identically to the givens. As well as making it clear where many border segments must be drawn - such as between any two differing numbers, or surrounding a region of matching numbers whose quantity is that number - it also permits the second part of the puzzle's rule to be visualized as simply "the same number cannot appear on both sides of a border", which greatly accelerates solving. A curious side effect of numbering every cell is that when the puzzle is completed, the numbers alone unambiguously define the solution, the actual borders being trivially deducible. This makes communication of a solution without a grid quite feasible; indeed, solutions for Allied Occupation give only the numbers. (Nikoli always publishes solutions to their Fillomino puzzles with both the polyomino borders drawn in and numbers given in every cell.)
The typical means of starting a Fillomino puzzle is to draw in the obvious borders between non-matching givens and surrounding all polyominoes completed by the givens alone ('1's, pairs of orthogonally adjacent '2's, and so on). From there, the solver searches for three things, possibly in combination:
Variants
Fillomino adapts to different geometries; hexagonal grids can be used, with the only change in the rules being replacing all instances of polyomino with polyhex. Another variant was published by Nikoli under the name NIKOJI; letters are used as givens instead of numbers, where the letters and polyominoes have a one-to-one correspondence and only matching letters have matching polyominoes (in size, shape, orientation, and letter position).
A computer-based variant of the game in which the player enters numbers (the computer draws the boundaries for the player) is known "Filling" and is part of the "SGT-Puzzles" package.
