Double groupoid

Definition

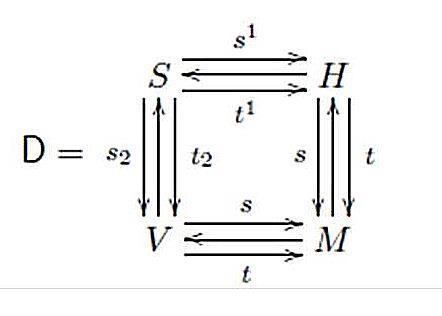
A double groupoid D is a higher-dimensional groupoid involving a relationship for both `horizontal' and `vertical' groupoid structures. (A double groupoid can also be considered as a generalization of certain higher-dimensional groups.) The geometry of squares and their compositions leads to a common representation of a double groupoid in the following diagram:

where M is a set of 'points', H and V are, respectively, 'horizontal' and 'vertical' groupoids, and S is a set of 'squares' with two compositions. The composition laws for a double groupoid D make it also describable as a groupoid internal to the category of groupoids.

Given two groupoids H and V over a set M, there is a double groupoid ◻ ( H , V ) with H,V as horizontal and vertical edge groupoids, and squares given by quadruples

for which one assumes always that h, h′ are in H and v, v′ are in V, and that the initial and final points of these edges match in M as suggested by the notation; that is for example sh = sv, th = sv', ..., etc. The compositions are to be inherited from those of H,V; that is:

and

This construction is the right adjoint to the forgetful functor which takes the double groupoid as above, to the pair of groupoids H,V over M.

Other related constructions are that of a double groupoid with connection and homotopy double groupoids. The homotopy double groupoid of a pair of pointed spaces is a key element of the proof of a two-dimensional Seifert-van Kampen Theorem, first proved by Brown and Higgins in 1978, and given an extensive treatment in the book.

Homotopy double groupoid

A generalisation to dimension 2 of the fundamental groupoid on a set of base was given by Brown and Higgins in 1978 as follows. Let ( X , A , C ) be a triple of spaces, i.e. C ⊆ A ⊆ X . Define ρ ( X , A , C ) to be the set of homotopy classes rel vertices of maps of a square into X which take the edges into A and the vertices into C. It is not entirely trivial to prove that the natural compositions of such squares in two directions are inherited by these homotopy classes to give a double groupoid, which also has an extra structure of so-called connections necessary to discuss the idea of commutative cube in a double groupoid. This double groupoid is used in an essential way to prove a two-dimensional Seifert-van Kampen theorem, which gives new information and computations on second relative homotopy groups as part of a crossed module. For more information, see Part I of the book by Brown, Higgins, Sivera listed below,.

Convolution algebra

A convolution C*-algebra of a double groupoid can also be constructed by employing the square diagram D of a double groupoid.

Double groupoid category

The category whose objects are double groupoids and whose morphisms are double groupoid homomorphisms that are double groupoid diagram (D) functors is called the double groupoid category, or the category of double groupoids.