In number theory, the divisor summatory function is a function that is a sum over the divisor function. It frequently occurs in the study of the asymptotic behaviour of the Riemann zeta function. The various studies of the behaviour of the divisor function are sometimes called divisor problems.
The divisor summatory function is defined as
D ( x ) = ∑ n ≤ x d ( n ) = ∑ j , k j k ≤ x 1 where
d ( n ) = σ 0 ( n ) = ∑ j , k j k = n 1 is the divisor function. The divisor function counts the number of ways that the integer n can be written as a product of two integers. More generally, one defines
D k ( x ) = ∑ n ≤ x d k ( n ) = ∑ m n ≤ x d k − 1 ( n ) where dk(n) counts the number of ways that n can be written as a product of k numbers. This quantity can be visualized as the count of the number of lattice points fenced off by a hyperbolic surface in k dimensions. Thus, for k=2, D(x) = D2(x) counts the number of points on a square lattice bounded on the left by the vertical-axis, on the bottom by the horizontal-axis, and to the upper-right by the hyperbola jk = x. Roughly, this shape may be envisioned as a hyperbolic simplex. This allows us to provide an alternative expression for D(x), and a simple way to compute it in O ( x ) time:
D ( x ) = ∑ k = 1 x ⌊ x k ⌋ = 2 ∑ k = 1 u ⌊ x k ⌋ − u 2 , where
u = ⌊ x ⌋ If the hyperbola in this context is replaced by a circle then determining the value of the resulting function is known as the Gauss circle problem.
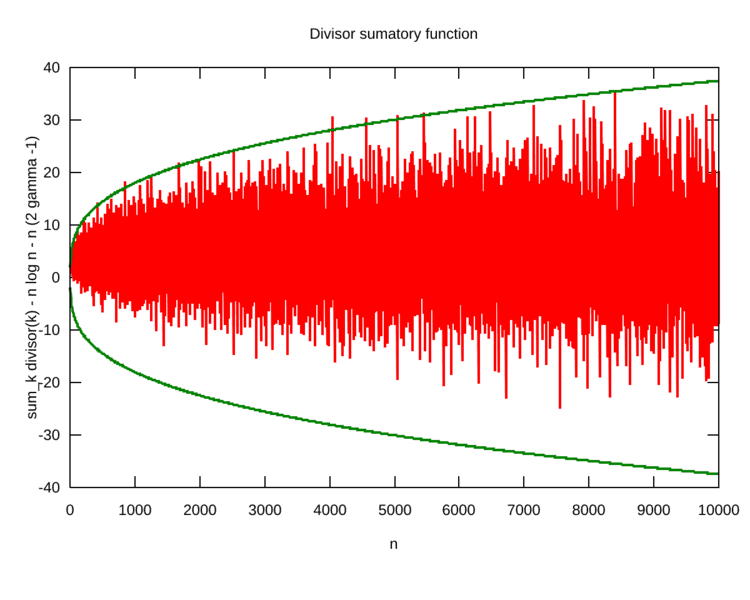
Finding a closed form for this summed expression seems to be beyond the techniques available, but it is possible to give approximations. The leading behaviour of the series is not difficult to obtain. Peter Gustav Lejeune Dirichlet demonstrated that
D ( x ) = x log x + x ( 2 γ − 1 ) + Δ ( x ) where γ is the Euler–Mascheroni constant, and the non-leading term is
Δ ( x ) = O ( x ) . Here, O denotes Big-O notation. The Dirichlet divisor problem, precisely stated, is to find the smallest value of θ for which
Δ ( x ) = O ( x θ + ϵ ) holds true, for any ϵ > 0 . As of today, this problem remains unsolved. Progress has been slow. Many of the same methods work for this problem and for Gauss's circle problem, another lattice-point counting problem. Section F1 of Unsolved Problems in Number Theory surveys what is known and not known about these problems.
In 1904, G. Voronoi proved that the error term can be improved to O ( x 1 / 3 log x ) . In 1916, G. H. Hardy showed that inf θ ≥ 1 / 4 . In particular, he demonstrated that for some constant K , there exist values of x for which Δ ( x ) > K x 1 / 4 and values of x for which Δ ( x ) < − K x 1 / 4 .In 1922, J. van der Corput improved Dirichlet's bound to inf θ ≤ 33 / 100. In 1928, J. van der Corput proved that inf θ ≤ 27 / 82. In 1950, Chih Tsung-tao and independently in 1953 H. E. Richert proved that inf θ ≤ 15 / 46. In 1969, Grigori Kolesnik demonstrated that inf θ ≤ 12 / 37 .In 1973, Grigori Kolesnik demonstrated that inf θ ≤ 346 / 1067 .In 1982, Grigori Kolesnik demonstrated that inf θ ≤ 35 / 108 .In 1988, H. Iwaniec and C. J. Mozzochi proved that inf θ ≤ 7 / 22. In 2003, M.N. Huxley improved this to show that inf θ ≤ 131 / 416. So, inf θ lies somewhere between 1/4 and 131/416 (approx. 0.3149); it is widely conjectured to be 1/4. Theoretical evidence lends credence to this conjecture, since Δ ( x ) / x 1 / 4 has a (non-Gaussian) limiting distribution. The value of 1/4 would also follow from a conjecture on exponent pairs.
In the generalized case, one has
D k ( x ) = x P k ( log x ) + Δ k ( x ) where P k is a polynomial of degree k − 1 . Using simple estimates, it is readily shown that
Δ k ( x ) = O ( x 1 − 1 / k log k − 2 x ) for integer k ≥ 2 . As in the k = 2 case, the infimum of the bound is not known for any value of k . Computing these infima is known as the Piltz divisor problem, after the name of the German mathematician Adolf Piltz (also see his German page). Defining the order α k as the smallest value for which Δ k ( x ) = O ( x α k + ε ) holds, for any ε > 0 , one has the following results (note that α 2 is the θ of the previous section):
α 2 ≤ 131 416 , α 3 ≤ 43 96 , and
α k ≤ 3 k − 4 4 k ( 4 ≤ k ≤ 8 ) α 9 ≤ 35 54 , α 10 ≤ 41 60 , α 11 ≤ 7 10 α k ≤ k − 2 k + 2 ( 12 ≤ k ≤ 25 ) α k ≤ k − 1 k + 4 ( 26 ≤ k ≤ 50 ) α k ≤ 31 k − 98 32 k ( 51 ≤ k ≤ 57 ) α k ≤ 7 k − 34 7 k ( k ≥ 58 ) E. C. Titchmarsh conjectures that α k = k − 1 2 k . Both portions may be expressed as Mellin transforms:
D ( x ) = 1 2 π i ∫ c − i ∞ c + i ∞ ζ 2 ( w ) x w w d w for c > 1 . Here, ζ ( s ) is the Riemann zeta function. Similarly, one has
Δ ( x ) = 1 2 π i ∫ c ′ − i ∞ c ′ + i ∞ ζ 2 ( w ) x w w d w with 0 < c ′ < 1 . The leading term of D ( x ) is obtained by shifting the contour past the double pole at w = 1 : the leading term is just the residue, by Cauchy's integral formula. In general, one has
D k ( x ) = 1 2 π i ∫ c − i ∞ c + i ∞ ζ k ( w ) x w w d w and likewise for Δ k ( x ) , for k ≥ 2 .