 | ||
Divergence and curl
In vector calculus, divergence is a vector operator that produces a signed scalar field giving the quantity of a vector field's source at each point. More technically, the divergence represents the volume density of the outward flux of a vector field from an infinitesimal volume around a given point.
Contents
- Divergence and curl
- Divergence 1 multivariable calculus khan academy
- Physical interpretation of divergence
- Definition in Cartesian coordinates
- Cylindrical coordinates
- Spherical coordinates
- Decomposition theorem
- Properties
- Relation with the exterior derivative
- Generalizations
- References
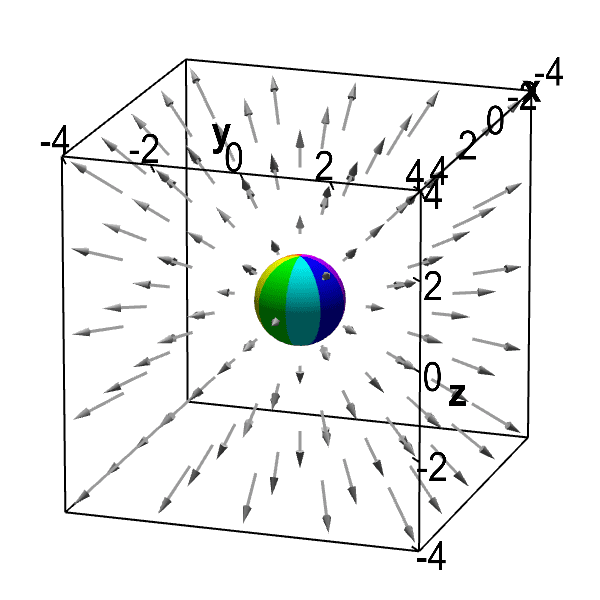
As an example, consider air as it is heated or cooled. The velocity of the air at each point defines a vector field. While air is heated in a region, it expands in all directions, and thus the velocity field points outward from that region. The divergence of the velocity field in that region would thus have a positive value. While the air is cooled and thus contracting, the divergence of the velocity has a negative value.

Divergence 1 multivariable calculus khan academy
Physical interpretation of divergence
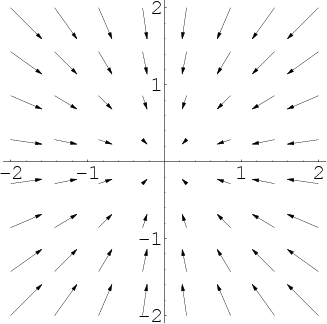
In physical terms, the divergence of a three-dimensional vector field is the extent to which the vector field flow behaves like a source at a given point. It is a local measure of its "outgoingness"– the extent to which there is more of some quantity exiting an infinitesimal region of space than entering it. If the divergence is nonzero at some point then there must be a source or sink at that position. (Note that we are imagining the vector field to be like the velocity vector field of a fluid (in motion) when we use the terms flow, source and so on.)
More rigorously, the divergence of a vector field F at a point p can be defined as the limit of the net flow of F across the smooth boundary of a three-dimensional region V divided by the volume of V as V shrinks to p. Formally,
where | V | is the volume of V, S(V) is the boundary of V, and the integral is a surface integral with n̂ being the outward unit normal to that surface. The result, div F, is a function of p. From this definition it also becomes obvious that div F can be seen as the source density of the flux of F.
In light of the physical interpretation, a vector field with zero divergence everywhere is called incompressible or solenoidal – in this case, no net flow can occur across any closed surface.
The intuition that the sum of all sources minus the sum of all sinks should give the net flow outwards of a region is made precise by the divergence theorem.
Definition in Cartesian coordinates
Let x, y, z be a system of Cartesian coordinates in 3-dimensional Euclidean space, and let i, j, k be the corresponding basis of unit vectors. The divergence of a continuously differentiable vector field F = Ui + Vj + Wk is defined as the scalar-valued function:
Although expressed in terms of coordinates, the result is invariant under rotations, as the physical interpretation suggests. More generally, the trace of the Jacobian matrix of an N-dimensional vector field F in N-dimensional space is invariant under any invertible linear transformation.
The common notation for the divergence ∇ · F is a convenient mnemonic, where the dot denotes an operation reminiscent of the dot product: take the components of the ∇ operator (see del), apply them to the components of F, and sum the results. Because applying an operator is different from multiplying the components, this is considered an abuse of notation.
The divergence of a continuously differentiable second-order tensor field ε is a first-order tensor field:
Cylindrical coordinates
For a vector expressed in cylindrical coordinates as
where ea is the unit vector in direction a, the divergence is
Spherical coordinates
In spherical coordinates, with θ the angle with the z axis and φ the rotation around the z axis, the divergence is
Decomposition theorem
It can be shown that any stationary flux v(r) that is at least twice continuously differentiable in ℝ3 and vanishes sufficiently fast for | r | → ∞ can be decomposed into an irrotational part E(r) and a source-free part B(r). Moreover, these parts are explicitly determined by the respective source densities (see above) and circulation densities (see the article Curl):
For the irrotational part one has
with
The source-free part, B, can be similarly written: one only has to replace the scalar potential Φ(r) by a vector potential A(r) and the terms −∇Φ by +∇ × A, and the source density div v by the circulation density ∇ × v.
This "decomposition theorem" is a by-product of the stationary case of electrodynamics. It is a special case of the more general Helmholtz decomposition which works in dimensions greater than three as well.
Properties
The following properties can all be derived from the ordinary differentiation rules of calculus. Most importantly, the divergence is a linear operator, i.e.
for all vector fields F and G and all real numbers a and b.
There is a product rule of the following type: if φ is a scalar-valued function and F is a vector field, then
or in more suggestive notation
Another product rule for the cross product of two vector fields F and G in three dimensions involves the curl and reads as follows:
or
The Laplacian of a scalar field is the divergence of the field's gradient:
The divergence of the curl of any vector field (in three dimensions) is equal to zero:
If a vector field F with zero divergence is defined on a ball in ℝ3, then there exists some vector field G on the ball with F = curl G. For regions in ℝ3 more topologically complicated than this, the latter statement might be false (see Poincaré lemma). The degree of failure of the truth of the statement, measured by the homology of the chain complex
{scalar fields on U } → {vector fields on U } → {vector fields on U } → {scalar fields on U }(where the first map is the gradient, the second is the curl, the third is the divergence) serves as a nice quantification of the complicatedness of the underlying region U. These are the beginnings and main motivations of de Rham cohomology.
Relation with the exterior derivative
One can express the divergence as a particular case of the exterior derivative, which takes a 2-form to a 3-form in ℝ3. Define the current two-form as
It measures the amount of "stuff" flowing through a surface per unit time in a "stuff fluid" of density ρ = 1 dx ∧ dy ∧ dz moving with local velocity F. Its exterior derivative dj is then given by
Thus, the divergence of the vector field F can be expressed as:
Here the superscript ♭ is one of the two musical isomorphisms, and ★ is the Hodge dual. Working with the current two-form and the exterior derivative is usually easier than working with the vector field and divergence, because unlike the divergence, the exterior derivative commutes with a change of (curvilinear) coordinate system.
Generalizations
The divergence of a vector field can be defined in any number of dimensions. If
in a Euclidean coordinate system where x = (x1, x2,... xn) and dx = (dx1, dx2,... dxn), define
The appropriate expression is more complicated in curvilinear coordinates.
In the case of one dimension, F reduces to a regular function, and the divergence reduces to the derivative.
For any n, the divergence is a linear operator, and it satisfies the "product rule"
for any scalar-valued function φ.
The divergence of a vector field extends naturally to any differentiable manifold of dimension n with a volume form (or density) μ, e.g. a Riemannian or Lorentzian manifold. Generalising the construction of a two-form for a vector field on ℝ3, on such a manifold a vector field X defines an (n − 1)-form j = iX μ obtained by contracting X with μ. The divergence is then the function defined by
Standard formulas for the Lie derivative allow us to reformulate this as
This means that the divergence measures the rate of expansion of a volume element as we let it flow with the vector field.
On a pseudo-Riemannian manifold, the divergence with respect to the metric volume form can be computed in terms of the Levi-Civita connection ∇:
where the second expression is the contraction of the vector field valued 1-form ∇X with itself and the last expression is the traditional coordinate expression from Ricci calculus.
An equivalent expression without using connection is
where g is the metric and ∂a denotes partial derivative with respect to coordinate xa.
Divergence can also be generalised to tensors. In Einstein notation, the divergence of a contravariant vector Fμ is given by
where ∇μ denotes the covariant derivative.
Equivalently, some authors define the divergence of a mixed tensor by using the musical isomorphism ♯: if T is a (p, q)-tensor (p for the contravariant vector and q for the covariant one), then we define the divergence of T to be the (p, q − 1)-tensor
that is we trace the covariant derivative on the first two covariant indices.
