Dirichlet process

Introduction

Dirichlet processes are usually used when modeling data that tends to repeat previous values in a "rich get richer" fashion. Specifically, suppose that the generation of values X 1 , X 2 , … can be simulated by the following algorithm.

Input: H (a probability distribution called base distribution), α (a positive real number called scaling parameter)

1. Draw X 1 from the distribution H .
2. For n > 1 :

a) With probability α α + n − 1 draw X n from H .

b) With probability n x α + n − 1 set X n = x , where n x is the number of previous observations X j , j < n , such that X j = x .

At the same time, another common model for data is that the observations X 1 , X 2 , … are assumed to be independent and identically distributed (i.i.d.) according to some distribution P . The goal in introducing Dirichlet processes is to be able to describe the procedure outlined above in this i.i.d. model.

The X 1 , X 2 , … observations are not independent, since we have to consider the previous results when generating the next value. They are, however, exchangeable. This fact can be shown by calculating the joint probability distribution of the observations and noticing that the resulting formula only depends on which x values occur among the observations and how many repetitions they each have. Because of this exchangeability, de Finetti's representation theorem applies and it implies that the observations X 1 , X 2 , … are conditionally independent given a (latent) distribution P . This P is a random variable itself and has a distribution. This distribution (over distributions) is called Dirichlet process ( D P ). In summary, this means that we get an equivalent procedure to the above algorithm:

1. Draw a distribution P from D P ( H , α )
2. Draw observations X 1 , X 2 … independently from P .

In practice, however, drawing a concrete distribution P is impossible, since its specification requires an infinite amount of information. This is a common phenomenon in the context of Bayesian non-parametric statistics where a typical task is to learn distributions on function spaces, which involve effectively infinitely many parameters. The key insight is that in many applications the infinite dimensional distributions appear only as an intermediary computational device and are not required for either the initial specification of prior beliefs or for the statement of the final inference. The Dirichlet process can be used to circumvent infinite computational requirements as described above.

Formal definition

Given a measurable set S, a base probability distribution H and a positive real number α , the Dirichlet process D P ( H , α ) is a stochastic process whose sample path (or realization, i.e. an infinite set of random variates drawn from the process) is a probability distribution over S and the following holds. For any measureable finite partition of S, say { B i } i = 1 n ,

if  X ∼ D P ( H , α ) then  ( X ( B 1 ) , … , X ( B n ) ) ∼ D i r ( α H ( B 1 ) , … , α H ( B n ) ) ,

where D i r denotes the Dirichlet distribution and the notation X ∼ D means that the random variable X is distributed according to the distribution D .

Alternative views

There are several equivalent views of the Dirichlet process. Besides the definition above, the Dirichlet process can be defined implicitly through de Finetti's theorem as described in the first section; this is often called the Chinese restaurant process. A third alternative is the stick-breaking process, which defines the Dirichlet process constructively by writing a distribution sampled from the process as f ( x ) = ∑ k = 1 ∞ β k δ x k ( x ) , where { x k } k = 1 ∞ are samples from the base distribution H , δ x k is an indicator function centered on x k (zero everywhere except for δ x k ( x k ) = 1 ) and the β k are defined by a recursive scheme that repeatedly samples from the beta distribution B e t a ( 1 , α ) .

Use in Dirichlet mixture models

To understand what Dirichlet processes are and the problem they solve we consider the example of data clustering. It is a common situation that data points are assumed to be distributed in a hierarchical fashion where each data point belongs to a (randomly chosen) cluster and the members of a cluster are further distributed randomly within that cluster.

Example 1

For example, we might be interested in how people will vote on a number of questions in an upcoming election. A reasonable model for this situation might be to classify each voter as a liberal, a conservative or a moderate and then model the event that a voter says “Yes” to any particular question as a Bernoulli random variable with probability dependent on which political cluster they belong to. By looking at how votes were cast in previous years on similar pieces of legislation one could fit a predictive model using a simple clustering algorithm such as k-means. That algorithm, however, requires knowing in advance the number of clusters that generated the data. In many situations it is not possible to determine this ahead of time, and even when we can reasonably assume a number of clusters we would still like to be able to check this assumption. For example, in the voting example above the division into liberal, conservative and moderate might not be finely tuned enough; attributes such as a religion, class or race could also be critical for modeling voter behavior.

Example 2

As another example, we might be interested in modeling the velocities of galaxies using a simple model assuming that the velocities are clustered, for instance by assuming each velocity is distributed according to the normal distribution v i ∼ N ( μ k , σ 2 ) , where the i th observation belongs to the k th cluster of galaxies with common expected velocity. In this case it is far from obvious how to determine a priori how many clusters (of common velocities) there should be and any model for this would be highly suspect and should be checked against the data. By using a Dirichlet process prior for the distribution of cluster means we circumvent the need to explicitly specify ahead of time how many clusters there are, although the concentration parameter still controls it implicitly.

We consider this example in more detail. A first naive model is to presuppose that there are K clusters of normally distributed velocities with common known fixed variance σ 2 . Denoting the event that the i th observation is in the k th cluster as z i = k we can write this model as:

( v i ∣ z i = k , μ k ) ∼ N ( μ k , σ 2 ) P ( z i = k ) = π k ( π ∣ α ) ∼ D i r ( α K ⋅ 1 K ) μ k ∼ H ( λ )

That is, we assume that the data belongs to K distinct clusters with means μ k and that π k is the (unknown) prior probability of a data point belonging to the k th cluster. We assume that we have no initial information distinguishing the clusters, which is captured by the symmetric prior D i r ( α / K ⋅ 1 K ) . Here D i r denotes the Dirichlet distribution and 1 K denotes a vector of length K where each element is 1. We further assign independent and identical prior distributions H ( λ ) to each of the cluster means, where H may be any parametric distribution with parameters denoted as λ . The hyper-parameters α and λ are taken to be known fixed constants, chosen to reflect our prior beliefs about the system. To understand the connection to Dirichlet process priors we rewrite this model in an equivalent but more suggestive form:

( v i ∣ μ ~ i ) ∼ N ( μ ~ i , σ 2 ) μ ~ i ∼ G = ∑ k = 1 K π k δ μ k ( μ ~ i ) ( π ∣ α ) ∼ D i r ( α K ⋅ 1 K ) μ k ∼ H ( λ )

Instead of imagining that each data point is first assigned a cluster and then drawn from the distribution associated to that cluster we now think of each observation being associated with parameter μ ~ i drawn from some discrete distribution G with support on the K means. That is, we are now treating the μ ~ i as being drawn from the random distribution G and our prior information is incorporated into the model by the distribution over distributions G .

We would now like to extend this model to work without pre-specifying a fixed number of clusters K . Mathematically, this means we would like to select a random prior distribution G ( μ ~ i ) = ∑ k = 1 ∞ π k δ μ k ( μ ~ i ) where the values of the clusters means μ k are again independently distributed according to H ( λ ) and the distribution over π k is symmetric over the infinite set of clusters. This is exactly what is accomplished by the model:

( v i ∣ μ ~ i ) ∼ N ( μ ~ i , σ 2 ) μ ~ i ∼ G G ∼ D P ( H ( λ ) , α )

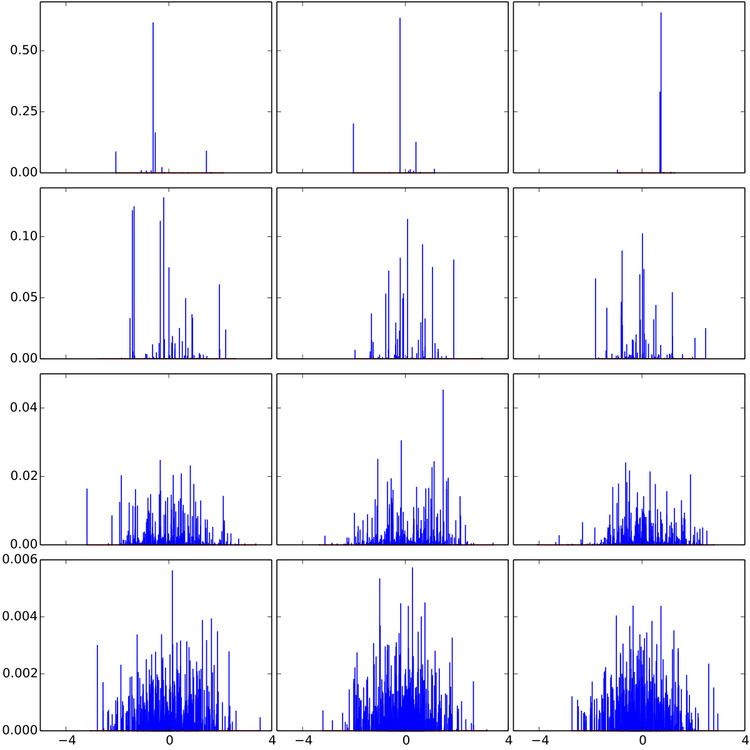
With this in hand we can better understand the computational merits of the Dirichlet process. Suppose that we wanted to draw n observations from the naive model with exactly K clusters. A simple algorithm for doing this would be to draw K values of μ k from H ( λ ) , a distribution π from D i r ( α / K ⋅ 1 K ) and then for each observation independently sample the cluster k with probability π k and the value of the observation according to N ( μ k , σ 2 ) . It is easy to see that this algorithm does not work in case where we allow infinite clusters because this would require sampling an infinite dimensional parameter π . However, as described above it is still possible to sample observations v i using the Chinese Restaurant algorithm, which avoids having to explicitly specify π but is still equivalent, as implied by de Finetti's representation theorem.

Fitting the model described above based on observed data D means finding the posterior distribution p ( π , μ ∣ D ) over cluster probabilities and their associated means. In the infinite dimensional case it is obviously impossible to write down the posterior explicitly. It is, however, possible to draw samples from this posterior using a modified Gibbs sampler. This is the critical fact that makes the Dirichlet process prior useful for inference.

The Chinese restaurant process

As shown above, a simple distribution, the so-called Chinese restaurant process, results from considering the conditional distribution of one component assignment given all previous ones in a Dirichlet distribution mixture model with K components, and then taking the limit as K goes to infinity. It can be shown, using the above formal definition of the Dirichlet process and considering the process-centered view, that the conditional distribution of the component assignment of one sample from the process given all previous samples follows a Chinese restaurant process.

Suppose that J samples, { θ j } j = 1 J have already been obtained. According to the Chinese restaurant process, the ( J + 1 ) t h sample should be drawn from

θ J + 1 ∼ 1 H ( S ) + J ( H + ∑ j = 1 J δ θ j )

where δ θ is an atomic distribution centered on θ . Interpreting this, two properties are clear:

1. Even if S is an uncountable set, there is a nonzero probability that two samples will have exactly the same value. Samples from a Dirichlet process are discrete.
2. The Dirichlet process exhibits a self-reinforcing property; the more often a given value has been sampled in the past, the more likely it is to be sampled again.

The name "Chinese restaurant process" is derived from the following analogy: imagine an infinitely large restaurant containing an infinite number of tables, and able to serve an infinite number of dishes. The restaurant in question operates a somewhat unusual seating policy whereby new diners are seated either at a currently occupied table with probability proportional to the number of guests already seated there, or at an empty table with probability proportional to a constant. Guests who sit at an occupied table must order the same dish as those currently seated, whereas guests allocated a new table are served a new dish at random. The distribution of dishes after J guests are served is a sample drawn as described above. The Chinese restaurant process is related to the Pólya urn sampling scheme for finite Dirichlet distributions.

The stick-breaking process

A third approach to the Dirichlet process is the so-called stick-breaking process view. Remember that draws from a Dirichlet process are distributions over a set S . As noted previously, the distribution drawn is discrete with probability 1. In the stick-breaking process view, we explicitly use the discreteness and give the probability mass function of this (random) discrete distribution as:

f ( θ ) = ∑ k = 1 ∞ β k ⋅ δ θ k ( θ )

where δ θ k is the indicator function which evaluates to zero everywhere, except for δ θ k ( θ k ) = 1 . Since this distribution is random itself, its mass function is parameterized by two sets of random variables: the locations { θ k } k = 1 ∞ and the corresponding probabilities { β k } k = 1 ∞ . In the following, we present without proof what these random variables are.

The locations θ k are independent and identically distributed according to H , the base distribution of the Dirichlet process. The probabilities β k are given by a procedure resembling the breaking of a unit-length stick (hence the name):

β k = β k ′ ⋅ ∏ i = 1 k − 1 ( 1 − β i ′ )

where β k ′ are independent random variables with the beta distribution B e t a ( 1 , α ) . The resemblance to 'stick-breaking' can be seen by considering β k as the length of a piece of a stick. We start with a unit-length stick and in each step we break off a portion of the remaining stick according to β k ′ and assign this broken-off piece to β k . The formula can be understood by noting that after the first k − 1 values have their portions assigned, the length of the remainder of the stick is ∏ i = 1 k − 1 ( 1 − β i ′ ) and this piece is broken according to β k ′ and gets assigned to β k .

The smaller α is, the less of the stick will be left for subsequent values (on average), yielding more concentrated distributions.

The Pólya urn scheme

Yet another way to visualize the Dirichlet process and Chinese restaurant process is as a modified Pólya urn scheme. Imagine that we start with an urn filled with α black balls. Then we proceed as follows:

1. Each time we need an observation, we draw a ball from the urn.
2. If the ball is black, we generate a new (non-black) color uniformly, label a new ball this color, drop the new ball into the urn along with the ball we drew, and return the color we generated.
3. Otherwise, label a new ball with the color of the ball we drew, drop the new ball into the urn along with the ball we drew, and return the color we observed.

The resulting distribution over colors is the same as the distribution over tables in the Chinese restaurant process. Furthermore, when we draw a black ball, if rather than generating a new color, we instead pick a random value from a base distribution H and use that value to label the new ball, the resulting distribution over labels will be the same as the distribution over values in a Dirichlet process.

Applications of the Dirichlet process

Dirichlet processes are frequently used in Bayesian nonparametric statistics. "Nonparametric" here does not mean a parameter-less model, rather a model in which representations grow as more data are observed. Bayesian nonparametric models have gained considerable popularity in the field of machine learning because of the above-mentioned flexibility, especially in unsupervised learning. In a Bayesian nonparametric model, the prior and posterior distributions are not parametric distributions, but stochastic processes. The fact that the Dirichlet distribution is a probability distribution on the simplex of sets of non-negative numbers that sum to one makes it a good candidate to model distributions over distributions or distributions over functions. Additionally, the nonparametric nature of this model makes it an ideal candidate for clustering problems where the distinct number of clusters is unknown beforehand.

As draws from a Dirichlet process are discrete, an important use is as a prior probability in infinite mixture models. In this case, S is the parametric set of component distributions. The generative process is therefore that a sample is drawn from a Dirichlet process, and for each data point in turn a value is drawn from this sample distribution and used as the component distribution for that data point. The fact that there is no limit to the number of distinct components which may be generated makes this kind of model appropriate for the case when the number of mixture components is not well-defined in advance. For example, the infinite mixture of Gaussians model.

The infinite nature of these models also lends them to natural language processing applications, where it is often desirable to treat the vocabulary as an infinite, discrete set.

The Dirichlet Process can also be used for nonparametric hypothesis testing, i.e. to develop Bayesian nonparametric versions of the classical nonparametric hypothesis tests, e.g. sign test, Wilcoxon rank sum test, Wilcoxon signed-rank test, etc. For instance, Bayesian nonparametric versions of the Wilcoxon rank sum test and the Wilcoxon signed-rank test have been developed by using the imprecise Dirichlet process, a prior ignorance Dirichlet process.

Related distributions

The Pitman–Yor process is a generalization of the Dirichlet process to accommodate power-law tails

The hierarchical Dirichlet process extends the ordinary Dirichlet process for modelling grouped data.