Difference of two squares

Proof

The proof of the factorization identity is straightforward. Starting from the left-hand side, apply the distributive law to get

By the commutative law, the middle two terms cancel:

leaving

The resulting identity is one of the most commonly used in mathematics. Among many uses, it gives a simple proof of the AM–GM inequality in two variables.

The proof just given indicates the scope of the identity in abstract algebra: it will hold in any commutative ring R.

Conversely, if this identity holds in a ring R for all pairs of elements a and b of the ring, then R is commutative. To see this, apply the distributive law to the right-hand side of the original equation and get

and for this to be equal to a 2 − b 2 , we must have

for all pairs a, b of elements of R, so the ring R is commutative.

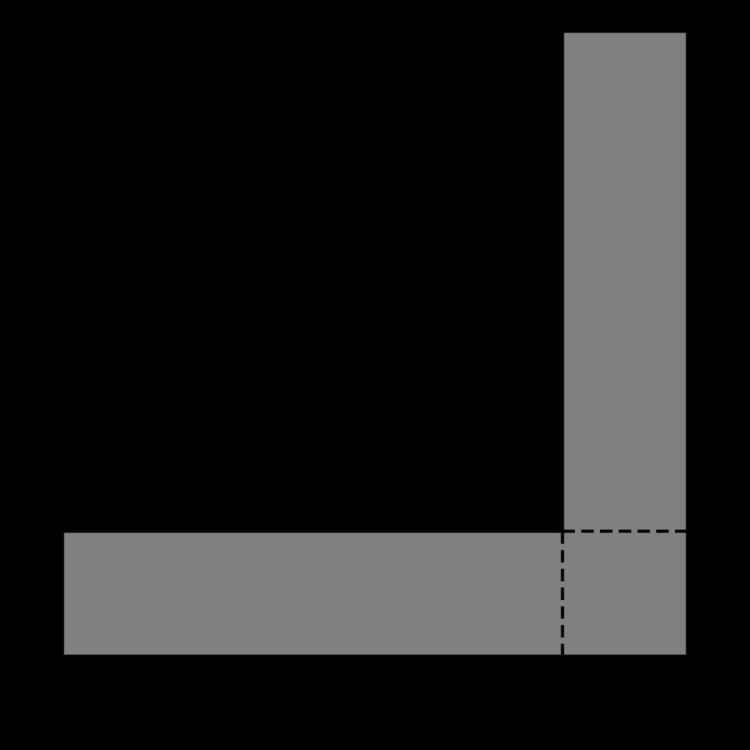
Geometrical demonstrations

The difference of two squares can also be illustrated geometrically as the difference of two square areas in a plane. In the diagram, the shaded part represents the difference between the areas of the two squares, i.e. a 2 − b 2 . The area of the shaded part can be found by adding the areas of the two rectangles; a ( a − b ) + b ( a − b ) , which can be factorized to ( a + b ) ( a − b ) . Therefore a 2 − b 2 = ( a + b ) ( a − b )

Another geometric proof proceeds as follows: We start with the figure shown in the first diagram below, a large square with a smaller square removed from it. The side of the entire square is a, and the side of the small removed square is b. The area of the shaded region is a 2 − b 2 . A cut is made, splitting the region into two rectangular pieces, as shown in the second diagram. The larger piece, at the top, has width a and height a-b. The smaller piece, at the bottom, has width a-b and height b. Now the smaller piece can be detached, rotated, and placed to the right of the larger piece. In this new arrangement, shown in the last diagram below, the two pieces together form a rectangle, whose width is a + b and whose height is a − b . This rectangle's area is ( a + b ) ( a − b ) . Since this rectangle came from rearranging the original figure, it must have the same area as the original figure. Therefore, a 2 − b 2 = ( a + b ) ( a − b ) .

Factorisation of polynomials

The formula for the difference of two squares can be used for factoring polynomials that contain the square of a first quantity minus the square of a second quantity. For example, the polynomial x 4 − 1 can be factored as follows:

As a second example, the first two terms of x 2 − y 2 + x − y can be factored as ( x + y ) ( x − y ) , so we have:

Complex number case: sum of two squares

The difference of two squares is used to find the linear factors of the sum of two squares, using complex number coefficients.

For example, the complex roots of z 2 + 4 can be found using difference of two squares:

Therefore the linear factors are ( z + 2 i ) and ( z − 2 i ) .

Since the two factors found by this method are complex conjugates, we can use this in reverse as a method of multiplying a complex number to get a real number. This is used to get real denominators in complex fractions.

Rationalising denominators

The difference of two squares can also be used in the rationalising of irrational denominators. This is a method for removing surds from expressions (or at least moving them), applying to division by some combinations involving square roots.

For example: The denominator of 5 3 + 4 can be rationalised as follows:

Here, the irrational denominator 3 + 4 has been rationalised to 13 .

Mental arithmetic

The difference of two squares can also be used as an arithmetical short cut. If you are multiplying two numbers whose average is a number which is easily squared the difference of two squares can be used to give you the product of the original two numbers.

For example:

Which means using the difference of two squares 27 × 33 can be restated as

Difference of two perfect squares

The difference of two consecutive perfect squares is the sum of the two bases n and n+1. This can be seen as follows:

Therefore the difference of two consecutive perfect squares is an odd number. Similarly, the difference of two arbitrary perfect squares is calculated as follows:

Therefore the difference of two even perfect squares is a multiple of 4 and the difference of two odd perfect squares is a multiple of 8.

Generalizations

The identity also holds in inner product spaces over the field of real numbers, such as for dot product of Euclidean vectors:

The proof is identical. By the way, assuming that a and b have equal norms (which means that their dot squares are equal), it demonstrates analytically the fact that two diagonals of a rhombus are perpendicular.

Difference of two nth powers

If a and b are two elements of a commutative ring R, then a n − b n = ( a − b ) ( ∑ k = 0 n − 1 a n − 1 − k b k ) . Note that binomial coefficients do not appear in the second factor, and the summation stops at n-1, not n.