Given the system:
f ( x ) = a 0 x n + a 1 x n − 1 + ⋯ + a n ( 1 ) = ( x − r 1 ) ( x − r 2 ) ⋯ ( x − r n ) ( 2 )
Assuming no roots of f ( x ) = 0 lie on the imaginary axis, and letting
N = The number of roots of
f ( x ) = 0 with negative real parts, and
P = The number of roots of
f ( x ) = 0 with positive real parts
then we have
N + P = n ( 3 )
Expressing f ( x ) in polar form, we have
f ( x ) = ρ ( x ) e j θ ( x ) ( 4 )
where
ρ ( x ) = R e 2 [ f ( x ) ] + I m 2 [ f ( x ) ] ( 5 )
and
θ ( x ) = tan − 1 ( I m [ f ( x ) ] / R e [ f ( x ) ] ) ( 6 )
from (2) note that
θ ( x ) = θ r 1 ( x ) + θ r 2 ( x ) + ⋯ + θ r n ( x ) ( 7 )
where
θ r i ( x ) = ∠ ( x − r i ) ( 8 )
Now if the ith root of f ( x ) = 0 has a positive real part, then (using the notation y=(RE[y],IM[y]))
θ r i ( x ) | x = j ∞ = ∠ ( x − r i ) | x = j ∞ = ∠ ( 0 − R e [ r i ] , ∞ − I m [ r i ] ) = ∠ ( − R e [ r i ] , ∞ ) = lim ϕ → − ∞ tan − 1 ϕ = − π 2 ( 9 )
and
θ r i ( x ) | x = − j ∞ = ∠ ( − R e [ r i ] , − ∞ ) = lim ϕ → ∞ tan − 1 ϕ = π 2 ( 10 )
Similarly, if the ith root of f ( x ) = 0 has a negative real part,
θ r i ( x ) | x = j ∞ = ∠ ( − R e [ r i ] , ∞ ) = lim ϕ → ∞ tan − 1 ϕ = π 2 ( 11 )
and
θ r i ( x ) | x = − j ∞ = ∠ ( − R e [ r i ] , − ∞ ) = lim ϕ → − ∞ tan − 1 ϕ = − π 2 ( 12 )
Therefore, θ r i ( x ) | x = − j ∞ x = j ∞ = − π when the ith root of f ( x ) has a positive real part, and θ r i ( x ) | x = − j ∞ x = j ∞ = π when the ith root of f ( x ) has a negative real part. Alternatively,
θ ( x ) | x = j ∞ = ∠ ( x − r 1 ) | x = j ∞ + ∠ ( x − r 2 ) | x = j ∞ + ⋯ + ∠ ( x − r n ) | x = j ∞ = π 2 N − π 2 P ( 13 )
and
θ ( x ) | x = − j ∞ = ∠ ( x − r 1 ) | x = − j ∞ + ∠ ( x − r 2 ) | x = − j ∞ + ⋯ + ∠ ( x − r n ) | x = − j ∞ = − π 2 N + π 2 P ( 14 )
So, if we define
Δ = 1 π θ ( x ) | − j ∞ j ∞ ( 15 )
then we have the relationship
N − P = Δ ( 16 )
and combining (3) and (16) gives us
N = n + Δ 2 and
P = n − Δ 2 ( 17 )
Therefore, given an equation of f ( x ) of degree n we need only evaluate this function Δ to determine N , the number of roots with negative real parts and P , the number of roots with positive real parts.
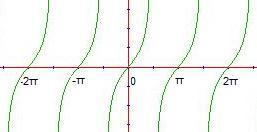
Equations (13) and (14) show that at x = ± ∞ , θ = θ ( x ) is an integer multiple of π / 2 . Note now, in accordance with (6) and Figure 1, the graph of tan ( θ ) vs θ , that varying x over an interval (a,b) where θ a = θ ( x ) | x = j a and θ b = θ ( x ) | x = j b are integer multiples of π , this variation causing the function θ ( x ) to have increased by π , indicates that in the course of travelling from point a to point b, θ has "jumped" from + ∞ to − ∞ one more time than it has jumped from − ∞ to + ∞ . Similarly, if we vary x over an interval (a,b) this variation causing θ ( x ) to have decreased by π , where again θ is a multiple of π at both x = j a and x = j b , implies that tan θ ( x ) = I m [ f ( x ) ] / R e [ f ( x ) ] has jumped from − ∞ to + ∞ one more time than it has jumped from + ∞ to − ∞ as x was varied over the said interval.
Thus, θ ( x ) | − j ∞ j ∞ is π times the difference between the number of points at which I m [ f ( x ) ] / R e [ f ( x ) ] jumps from − ∞ to + ∞ and the number of points at which I m [ f ( x ) ] / R e [ f ( x ) ] jumps from + ∞ to − ∞ as x ranges over the interval ( − j ∞ , + j ∞ ) provided that at x = ± j ∞ , tan [ θ ( x ) ] is defined.
In the case where the starting point is on an incongruity (i.e. θ a = π / 2 ± i π , i = 0, 1, 2, ...) the ending point will be on an incongruity as well, by equation (16) (since N is an integer and P is an integer, Δ will be an integer). In this case, we can achieve this same index (difference in positive and negative jumps) by shifting the axes of the tangent function by π / 2 , through adding π / 2 to θ . Thus, our index is now fully defined for any combination of coefficients in f ( x ) by evaluating tan [ θ ] = I m [ f ( x ) ] / R e [ f ( x ) ] over the interval (a,b) = ( + j ∞ , − j ∞ ) when our starting (and thus ending) point is not an incongruity, and by evaluating
tan [ θ ′ ( x ) ] = tan [ θ + π / 2 ] = − cot [ θ ( x ) ] = − R e [ f ( x ) ] / I m [ f ( x ) ] ( 18 )
over said interval when our starting point is at an incongruity.
This difference, Δ , of negative and positive jumping incongruities encountered while traversing x from − j ∞ to + j ∞ is called the Cauchy Index of the tangent of the phase angle, the phase angle being θ ( x ) or θ ′ ( x ) , depending as θ a is an integer multiple of π or not.
To derive Routh's criterion, first we will use a different notation to differentiate between the even and odd terms of f ( x ) :
f ( x ) = a 0 x n + b 0 x n − 1 + a 1 x n − 2 + b 1 x n − 3 + ⋯ ( 19 ) Now we have:
f ( j ω ) = a 0 ( j ω ) n + b 0 ( j ω ) n − 1 + a 1 ( j ω ) n − 2 + b 1 ( j ω ) n − 3 + ⋯ ( 20 ) = a 0 ( j ω ) n + a 1 ( j ω ) n − 2 + a 2 ( j ω ) n − 4 + ⋯ ( 21 ) + b 0 ( j ω ) n − 1 + b 1 ( j ω ) n − 3 + b 2 ( j ω ) n − 5 + ⋯ Therefore, if n is even,
f ( j ω ) = ( − 1 ) n / 2 [ a 0 ω n + a 1 ω n − 2 + a 2 ω n − 4 + ⋯ ] ( 22 ) + j ( − 1 ) ( n / 2 ) − 1 [ b 0 ω n − 1 + b 1 ω n − 3 + b 2 ω n − 5 + ⋯ ] and if n is odd:
f ( j ω ) = j ( − 1 ) ( n − 1 ) / 2 [ a 0 ω n + a 1 ω n − 2 + a 2 ω n − 4 + ⋯ ] ( 23 ) + ( − 1 ) ( n − 1 ) / 2 [ b 0 ω n − 1 + b 1 ω n − 3 + b 2 ω n − 5 + ⋯ ] Now observe that if n is an odd integer, then by (3) N + P is odd. If N + P is an odd integer, then N − P is odd as well. Similarly, this same argument shows that when n is even, N − P will be even. Equation (13) shows that if N − P is even, θ is an integer multiple of π . Therefore, tan ( θ ) is defined for n even, and is thus the proper index to use when n is even, and similarly tan ( θ ′ ) = tan ( θ + π ) = − cot ( θ ) is defined for n odd, making it the proper index in this latter case.
Thus, from (6) and (22), for n even:
Δ = I − ∞ + ∞ − I m [ f ( x ) ] R e [ f ( x ) ] = I − ∞ + ∞ b 0 ω n − 1 − b 1 ω n − 3 + ⋯ a 0 ω n − a 1 ω n − 2 + … ( 24 ) and from (18) and (23), for n odd:
Δ = I − ∞ + ∞ R e [ f ( x ) ] I m [ f ( x ) ] = I − ∞ + ∞ b 0 ω n − 1 − b 1 ω n − 3 + … a 0 ω n − a 1 ω n − 2 + … ( 25 ) Thus we are evaluating the same Cauchy index for both:
Δ = I − ∞ + ∞ b 0 ω n − 1 − b 1 ω n − 3 + … a 0 ω n − a 1 ω n − 2 + … ( 26 ) Sturm gives us a method for evaluating Δ = I − ∞ + ∞ f 2 ( x ) f 1 ( x ) . His theorem states as follows:
Given a sequence of polynomials f 1 ( x ) , f 2 ( x ) , … , f m ( x ) where:
1) If f k ( x ) = 0 then f k − 1 ( x ) ≠ 0 , f k + 1 ( x ) ≠ 0 , and sign [ f k − 1 ( x ) ] = − sign [ f k + 1 ( x ) ]
2) f m ( x ) ≠ 0 for − ∞ < x < ∞
and we define V ( x ) as the number of changes of sign in the sequence f 1 ( x ) , f 2 ( x ) , … , f m ( x ) for a fixed value of x , then:
Δ = I − ∞ + ∞ f 2 ( x ) f 1 ( x ) = V ( − ∞ ) − V ( + ∞ ) ( 27 )
A sequence satisfying these requirements is obtained using the Euclidean algorithm, which is as follows:
Starting with f 1 ( x ) and f 2 ( x ) , and denoting the remainder of f 1 ( x ) / f 2 ( x ) by f 3 ( x ) and similarly denoting the remainder of f 2 ( x ) / f 3 ( x ) by f 4 ( x ) , and so on, we obtain the relationships:
f 1 ( x ) = q 1 ( x ) f 2 ( x ) − f 3 ( x ) ( 28 ) f 2 ( x ) = q 2 ( x ) f 3 ( x ) − f 4 ( x ) … f m − 1 ( x ) = q m − 1 ( x ) f m ( x )
or in general
f k − 1 ( x ) = q k − 1 ( x ) f k ( x ) − f k + 1 ( x )
where the last non-zero remainder, f m ( x ) will therefore be the highest common factor of f 1 ( x ) , f 2 ( x ) , … , f m − 1 ( x ) . It can be observed that the sequence so constructed will satisfy the conditions of Sturm's theorem, and thus an algorithm for determining the stated index has been developed.
It is in applying Sturm's theorem (28) to (26), through the use of the Euclidean algorithm above that the Routh matrix is formed.
We get
f 3 ( ω ) = a 0 b 0 f 2 ( ω ) − f 1 ( ω ) ( 29 )
and identifying the coefficients of this remainder by c 0 , − c 1 , c 2 , − c 3 , and so forth, makes our formed remainder
f 3 ( ω ) = c 0 ω n − 2 − c 1 ω n − 4 + c 2 ω n − 6 − ⋯ ( 30 )
where
c 0 = a 1 − a 0 b 0 b 1 = b 0 a 1 − a 1 b 0 b 0 ; c 1 = a 2 − a 0 b 0 b 2 = b 0 a 2 − a 0 b 2 b 0 ; … ( 31 )
Continuing with the Euclidean algorithm on these new coefficients gives us
f 4 ( ω ) = b 0 c 0 f 3 ( ω ) − f 2 ( ω ) ( 32 )
where we again denote the coefficients of the remainder f 4 ( ω ) by d 0 , − d 1 , d 2 , − d 3 ,
making our formed remainder
f 4 ( ω ) = d 0 ω n − 3 − d 1 ω n − 5 + d 2 ω n − 7 − ⋯ ( 33 )
and giving us
d 0 = b 1 − b 0 c 0 c 1 = c 0 b 1 − b 1 c 0 c 0 ; d 1 = b 2 − b 0 c 0 c 2 = c 0 b 2 − b 0 c 2 c 0 ; … ( 34 )
The rows of the Routh array are determined exactly by this algorithm when applied to the coefficients of (19). An observation worthy of note is that in the regular case the polynomials f 1 ( ω ) and f 2 ( ω ) have as the highest common factor f n + 1 ( ω ) and thus there will be n polynomials in the chain f 1 ( x ) , f 2 ( x ) , … , f m ( x ) .
Note now, that in determining the signs of the members of the sequence of polynomials f 1 ( x ) , f 2 ( x ) , … , f m ( x ) that at ω = ± ∞ the dominating power of ω will be the first term of each of these polynomials, and thus only these coefficients corresponding to the highest powers of ω in f 1 ( x ) , f 2 ( x ) , … , and f m ( x ) , which are a 0 , b 0 , c 0 , d 0 , ... determine the signs of f 1 ( x ) , f 2 ( x ) , ..., f m ( x ) at ω = ± ∞ .
So we get V ( + ∞ ) = V ( a 0 , b 0 , c 0 , d 0 , … ) that is, V ( + ∞ ) is the number of changes of sign in the sequence a 0 ∞ n , b 0 ∞ n − 1 , c 0 ∞ n − 2 , ... which is the number of sign changes in the sequence a 0 , b 0 , c 0 , d 0 , ... and V ( − ∞ ) = V ( a 0 , − b 0 , c 0 , − d 0 , . . . ) ; that is V ( − ∞ ) is the number of changes of sign in the sequence a 0 ( − ∞ ) n , b 0 ( − ∞ ) n − 1 , c 0 ( − ∞ ) n − 2 , ... which is the number of sign changes in the sequence a 0 , − b 0 , c 0 , − d 0 , ...
Since our chain a 0 , b 0 , c 0 , d 0 , ... will have n members it is clear that V ( + ∞ ) + V ( − ∞ ) = n since within V ( a 0 , b 0 , c 0 , d 0 , … ) if going from a 0 to b 0 a sign change has not occurred, within V ( a 0 , − b 0 , c 0 , − d 0 , … ) going from a 0 to − b 0 one has, and likewise for all n transitions (there will be no terms equal to zero) giving us n total sign changes.
As Δ = V ( − ∞ ) − V ( + ∞ ) and n = V ( + ∞ ) + V ( − ∞ ) , and from (17) P = ( n − Δ / 2 ) , we have that P = V ( + ∞ ) = V ( a 0 , b 0 , c 0 , d 0 , … ) and have derived Routh's theorem -
The number of roots of a real polynomial f ( z ) which lie in the right half plane R e ( r i ) > 0 is equal to the number of changes of sign in the first column of the Routh scheme.
And for the stable case where P = 0 then V ( a 0 , b 0 , c 0 , d 0 , … ) = 0 by which we have Routh's famous criterion:
In order for all the roots of the polynomial f ( z ) to have negative real parts, it is necessary and sufficient that all of the elements in the first column of the Routh scheme be different from zero and of the same sign.