In mathematical analysis, the Cauchy index is an integer associated to a real rational function over an interval. By the Routh–Hurwitz theorem, we have the following interpretation: the Cauchy index of
r(
x) =
p(
x)/
q(
x)
over the real line is the difference between the number of roots of f(z) located in the right half-plane and those located in the left half-plane. The complex polynomial f(z) is such that
f(
iy) =
q(
y) +
ip(
y).
We must also assume that p has degree less than the degree of q.
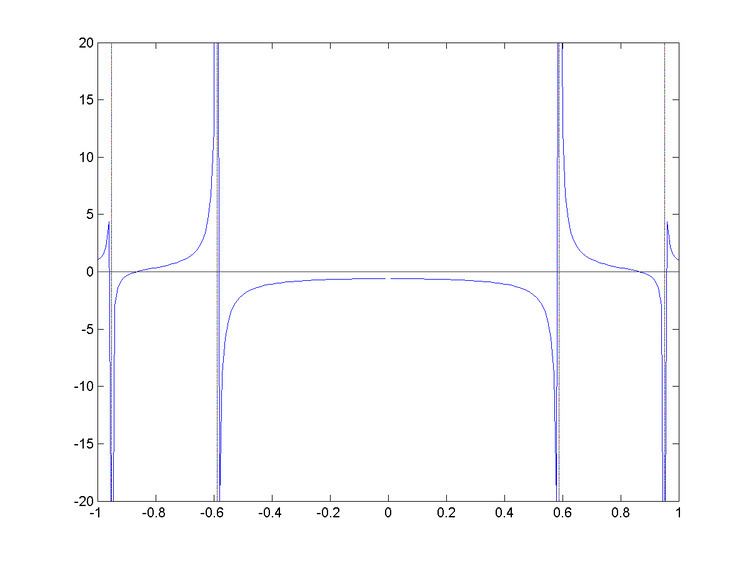
The Cauchy index was first defined for a pole s of the rational function r by Augustin Louis Cauchy in 1837 using one-sided limits as: I s r = { + 1 , if lim x ↑ s r ( x ) = − ∞ ∧ lim x ↓ s r ( x ) = + ∞ , − 1 , if lim x ↑ s r ( x ) = + ∞ ∧ lim x ↓ s r ( x ) = − ∞ , 0 , otherwise. A generalization over the compact interval [a,b] is direct (when neither a nor b are poles of r(x)): it is the sum of the Cauchy indices I s of r for each s located in the interval. We usually denote it by I a b r .We can then generalize to intervals of type [ − ∞ , + ∞ ] since the number of poles of r is a finite number (by taking the limit of the Cauchy index over [a,b] for a and b going to infinity).Consider the rational function: r ( x ) = 4 x 3 − 3 x 16 x 5 − 20 x 3 + 5 x = p ( x ) q ( x ) . We recognize in p(x) and q(x) respectively the Chebyshev polynomials of degree 3 and 5. Therefore r(x) has poles x 1 = 0.9511 , x 2 = 0.5878 , x 3 = 0 , x 4 = − 0.5878 and x 5 = − 0.9511 , i.e. x j = cos ( ( 2 i − 1 ) π / 2 n ) for j = 1 , . . . , 5 . We can see on the picture that I x 1 r = I x 2 r = 1 and I x 4 r = I x 5 r = − 1 . For the pole in zero, we have I x 3 r = 0 since the left and right limits are equal (which is because p(x) also has a root in zero). We conclude that I − 1 1 r = 0 = I − ∞ + ∞ r since q(x) has only five roots, all in [−1,1]. We cannot use here the Routh–Hurwitz theorem as each complex polynomial with f(iy) = q(y) + ip(y) has a zero on the imaginary line (namely at the origin).