DeGroot learning

Setup and the learning process

Take a society of n agents where everybody has an opinion on a subject, represented by a vector of probabilities p ( 0 ) = ( p 1 ( 0 ) , … , p n ( 0 ) ) . Agents obtain no new information based on which they can update their opinions but they communicate with other agents. Links between agents (who knows whom) and the weight they put on each other's opinions is represented by a trust matrix T where T i j is the weight that agent i puts on agent j 's opinion. The trust matrix is thus in a one-to-one relationship with a weighted, directed graph where there is an edge between i and j if and only if T i j > 0 . The trust matrix is stochastic, its rows consists of nonnegative real numbers, with each row summing to 1.

Formally, the beliefs are updated in each period as

so the t th period opinions are related to the initial opinions by

Convergence of beliefs and consensus

An important question is whether beliefs converge to a limit and to each other in the long run. As the trust matrix is stochastic, standard results in Markov chain theory can be used to state conditions under which the limit

exists for any initial beliefs p ( 0 ) ∈ [ 0 , 1 ] n . The following cases are treated in Golub and Jackson (2010).

Strongly connected case

If the social network graph (represented by the trust matrix) is strongly connected, convergence of beliefs is equivalent to each of the followings

entries sum to 1 such that, for every p ∈ [ 0 , 1 ] n , ( lim t → ∞ T t p ) i = s ⋅ p

for every i ∈ { 1 , … , n } where ⋅ denotes the dot product.

General case

It is not necessary to have a strongly connected social network to have convergent beliefs, however, the equality of limiting beliefs does not hold in general.

We say that a group of agents C ⊆ { 1 , … , n } is closed if for any i ∈ C , T i j > 0 only if j ∈ C . Beliefs are convergent if and only if every set of nodes (representing individuals) that is strongly connected and closed is also aperiodic.

Consensus

A group C of individuals is said to reach a consensus if p i ( ∞ ) = p j ( ∞ ) for any i , j ∈ C . This means that, as a result of the learning process, in the limit they have the same belief on the subject.

With a strongly connected and aperiodic network the whole group reaches a consensus. In general, any strongly connected and closed group C of individuals reaches a consensus for every initial vector of beliefs if and only if it is aperiodic. If, for example, there are two groups satisfying these assumptions, they reach a consensus inside the groups but there is not necessarily a consensus at the society level.

Social influence

Take a strongly connected and aperiodic social network. In this case, the common limiting belief is determined by the initial beliefs through

where s is the unique unit length left eigenvector of T corresponding to the eigenvalue 1. The vector s shows the weights that agents put on each other's initial beliefs in the consensus limit. Thus, the higher is s i , the more influence individual i has on the consensus belief.

The eigenvector property s = s T implies that

This means that the influence of i is a weighted average of those agents' influence s j who pay attention to i , with weights of their level of trust. Hence influential agents are characterized by being trusted by other individuals with high influence.

Examples

These examples appear in Jackson (2008).

Convergence of beliefs

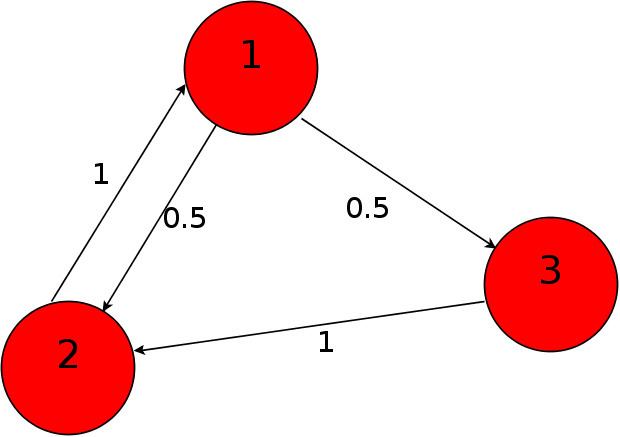
Consider a three-individual society with the following trust matrix:

Hence the first person weights the beliefs of the other two with equally, while the second listens only to the first, the third only to the second individual. For this social trust structure, the limit exists and equals

so the influence vector is s = ( 2 / 5 , 2 / 5 , 1 / 5 ) and the consensus belief is 2 / 5 p 1 ( 0 ) + 2 / 5 p 2 ( 0 ) + 1 / 5 p 3 ( 0 ) . In words, independently of the initial beliefs, individuals reach a consensus where the initial belief of the first and the second person has twice as high influence than the third one's.

Non-convergent beliefs

If we change the previous example such that the third person also listens exclusively to the first one, we have the following trust matrix:

In this case for any k ≥ 1 we have

and

so lim t → ∞ T t does not exist and beliefs do not converge in the limit. Intuitively, 1 is updating based on 2 and 3's beliefs while 2 and 3 update solely based on 1's belief so they interchange their beliefs in each period.

Asymptotic properties in large societies: wisdom

It is possible to examine the outcome of the DeGroot learning process in large societies, that is, in the n → ∞ limit.

Let the subject on which people have opinions be a "true state" μ ∈ [ 0 , 1 ] . Assume that individuals have independent noisy signals p i ( 0 ) ( n ) of μ (now superscript refers to time, the argument to the size of the society). Assume that for all n the trust matrix T ( n ) is such that the limiting beliefs p i ( ∞ ) ( n ) exists independently from the initial beliefs. Then the sequence of societies ( T ( n ) ) n = 1 ∞ is called wise if

where →   p   denotes convergence in probability. This means that if the society grows without bound, over time they will have a common and accurate belief on the uncertain subject.

A necessary and sufficient condition for wisdom can be given with the help of influence vectors. A sequence of societies is wise if and only if

that is, the society is wise precisely when even the most influential individual's influence vanishes in the large society limit. For further characterization and examples see Golub and Jackson (2010).