In mathematics, the Dawson function or Dawson integral (named after H. G. Dawson) is either
F ( x ) = D + ( x ) = e − x 2 ∫ 0 x e t 2 d t ,
also denoted as F(x) or D(x), or alternatively
D − ( x ) = e x 2 ∫ 0 x e − t 2 d t .
The Dawson function is the one-sided Fourier-Laplace sine transform of the Gaussian function,
D + ( x ) = 1 2 ∫ 0 ∞ e − t 2 / 4 sin ( x t ) d t . It is closely related to the error function erf, as
D + ( x ) = π 2 e − x 2 e r f i ( x ) = − i π 2 e − x 2 e r f ( i x ) where erfi is the imaginary error function, erfi(x) = −i erf(ix). Similarly,
D − ( x ) = π 2 e x 2 e r f ( x ) in terms of the real error function, erf.
In terms of either erfi or the Faddeeva function w(z), the Dawson function can be extended to the entire complex plane:
F ( z ) = π 2 e − z 2 e r f i ( z ) = i π 2 [ e − z 2 − w ( z ) ] ,
which simplifies to
D + ( x ) = F ( x ) = π 2 Im [ w ( x ) ] D − ( x ) = i F ( − i x ) = − π 2 [ e x 2 − w ( − i x ) ] for real x.
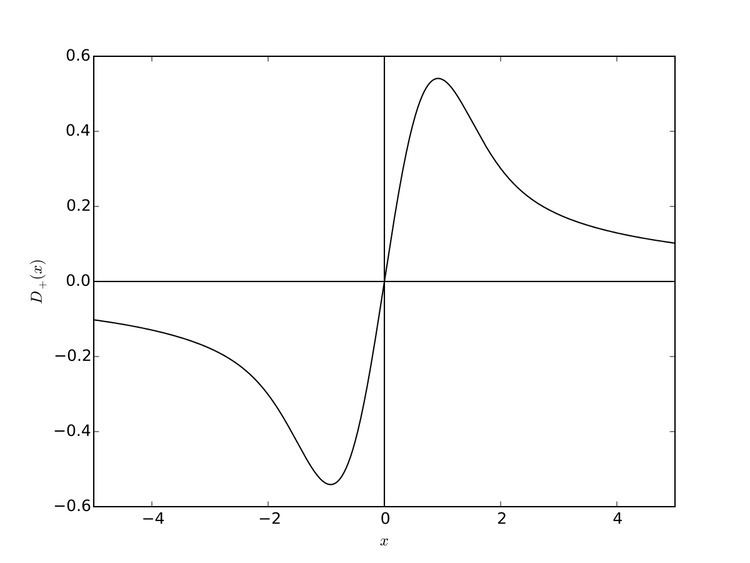
For |x| near zero, F(x) ≈ x, and for |x| large, F(x) ≈ 1/(2x). More specifically, near the origin it has the series expansion
F ( x ) = ∑ k = 0 ∞ ( − 1 ) k 2 k ( 2 k + 1 ) ! ! x 2 k + 1 = x − 2 3 x 3 + 4 15 x 5 − ⋯ ,
while for large x it has the asymptotic expansion
F ( x ) = ∑ k = 0 ∞ ( 2 k − 1 ) ! ! 2 k + 1 x 2 k + 1 = 1 2 x + 1 4 x 3 + 3 8 x 5 + ⋯ ,
where n!! is the double factorial.
F(x) satisfies the differential equation
d F d x + 2 x F = 1 with the initial condition F(0) = 0. Consequently, it has extrema for
F ( x ) = 1 2 x ,
resulting in x = ±0.92413887… ( A133841), F(x) = ±0.54104422… ( A133842).
Inflection points follow for
F ( x ) = x 2 x 2 − 1 ,
resulting in x = ±1.50197526… ( A133843), F(x) = ±0.42768661… ( A245262). (Apart from the trivial inflection point at x = 0, F(x) = 0.)
The Hilbert Transform of the Gaussian is defined as
H ( y ) = π − 1 P . V . ∫ − ∞ ∞ e − x 2 y − x d x P.V. denotes the Cauchy principal value, and we restrict ourselves to real y . H ( y ) can be related to the Dawson function as follows. Inside a principal value integral, we can treat 1 / u as a generalized function or distribution, and use the Fourier representation
1 u = ∫ 0 ∞ d k sin k u = ∫ 0 ∞ d k Im e i k u With 1 / u = 1 / ( y − x ) , we use the exponential representation of sin ( k u ) and complete the square with respect to x to find
π H ( y ) = Im ∫ 0 ∞ d k exp [ − k 2 / 4 + i k y ] ∫ − ∞ ∞ d x exp [ − ( x + i k / 2 ) 2 ] We can shift the integral over x to the real axis, and it gives π 1 / 2 . Thus
π 1 / 2 H ( y ) = Im ∫ 0 ∞ d k exp [ − k 2 / 4 + i k y ] We complete the square with respect to k and obtain
π 1 / 2 H ( y ) = e − y 2 Im ∫ 0 ∞ d k exp [ − ( k / 2 − i y ) 2 ] We change variables to u = i k / 2 + y :
π 1 / 2 H ( y ) = − 2 e − y 2 Im ∫ y i ∞ + y d u e u 2 The integral can be performed as a contour integral around a rectangle in the complex plane. Taking the imaginary part of the result gives
H ( y ) = 2 π − 1 / 2 F ( y ) where F ( y ) is the Dawson function as defined above.
The Hilbert transform of x 2 n e − x 2 is also related to the Dawson function. We see this with the technique of differentiating inside the integral sign. Let
H n = π − 1 P . V . ∫ − ∞ ∞ x 2 n e − x 2 y − x d x Introduce
H a = π − 1 P . V . ∫ − ∞ ∞ e − a x 2 y − x d x The nth derivative is
∂ n H a ∂ a n = ( − 1 ) n π − 1 P . V . ∫ − ∞ ∞ x 2 n e − a x 2 y − x d x We thus find
H n = ( − 1 ) n ∂ n H a ∂ a n | a = 1 The derivatives are performed first, then the result evaluated at a = 1 . A change of variable also gives H a = 2 π − 1 / 2 F ( y a ) . Since F ′ ( y ) = 1 − 2 y F ( y ) , we can write H n = P 1 ( y ) + P 2 ( y ) F ( y ) where P 1 and P 2 are polynomials. For example, H 1 = − π − 1 / 2 y + 2 π − 1 / 2 y 2 F ( y ) . Alternatively, H n can be calculated using the recurrence relation (for n ≥ 0 )
H n + 1 ( y ) = y 2 H n ( y ) − ( 2 n − 1 ) ! ! π 2 n y .