Rahul Sharma (Editor)

Data stream clustering

Updated on
Edit
Like
Comment
Share on FacebookTweet on TwitterShare on LinkedInShare on Reddit
Data stream clustering

In computer science, data stream clustering is defined as the clustering of data that arrive continuously such as telephone records, multimedia data, financial transactions etc. Data stream clustering is usually studied as a streaming algorithm and the objective is, given a sequence of points, to construct a good clustering of the stream, using a small amount of memory and time.

Contents

History

Data stream clustering has recently attracted attention for emerging applications that involve large amounts of streaming data. For clustering, k-means is a widely used heuristic but alternate algorithms have also been developed such as k-medoids, CURE and the popular BIRCH. For data streams, one of the first results appeared in 1980 but the model was formalized in 1998.

Definition

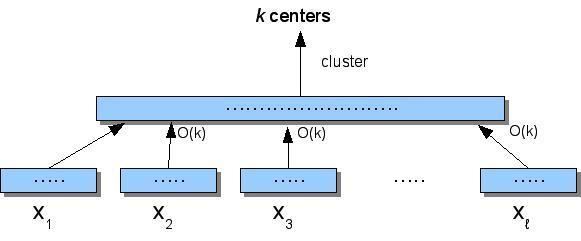
The problem of data stream clustering is defined as:

Input: a sequence of n points in metric space and an integer k.
Output: k centers in the set of the n points so as to minimize the sum of distances from data points to their closest cluster centers.

This is the streaming version of the k-median problem.

STREAM

STREAM is an algorithm for clustering data streams described by Guha, Mishra, Motwani and O'Callaghan which achieves a constant factor approximation for the k-Median problem in a single pass and using small space.

Theorem: STREAM can solve the k-Median problem on a data stream in a single pass, with time O(n1+e) and space θ(nε) up to a factor 2O(1/e), where n the number of points and e<1/2.

To understand STREAM, the first step is to show that clustering can take place in small space (not caring about the number of passes). Small-Space is a divide-and-conquer algorithm that divides the data, S, into ℓ pieces, clusters each one of them (using k-means) and then clusters the centers obtained.

Algorithm Small-Space(S)

Where, if in Step 2 we run a bicriteria (a,b)-approximation algorithm which outputs at most ak medians with cost at most b times the optimum k-Median solution and in Step 4 we run a c-approximation algorithm then the approximation factor of Small-Space() algorithm is 2c(1+2b)+2b. We can also generalize Small-Space so that it recursively calls itself i times on a successively smaller set of weighted centers and achieves a constant factor approximation to the k-median problem.

The problem with the Small-Space is that the number of subsets ℓ that we partition S into is limited, since it has to store in memory the intermediate medians in X'. So, if M is the size of memory, we need to partition S into ℓ subsets such that each subset fits in memory, (n/ ℓ ) and so that the weighted ℓ k centers also fit in memory, ℓ k<M. But such an ℓ may not always exist.

The STREAM algorithm solves the problem of storing intermediate medians and achieves better running time and space requirements. The algorithm works as follows:

Other Algorithms

Other well-known algorithms used for data stream clustering are:

  • BIRCH: builds a hierarchical data structure to incrementally cluster the incoming points using the available memory and minimizing the amount of I/O required. The complexity of the algorithm is O(N) since one pass suffices to get a good clustering (though, results can be improved by allowing several passes).
  • COBWEB: is an incremental clustering technique that keeps a hierarchical clustering model in the form of a classification tree. For each new point COBWEB descends the tree, updates the nodes along the way and looks for the best node to put the point on (using a category utility function).
  • C2ICM: builds a flat partitioning clustering structure by selecting some objects as cluster seeds/initiators and a non-seed is assigned to the seed that provides the highest coverage, addition of new objects can introduce new seeds and falsify some existing old seeds, during incremental clustering new objects and the members of the falsified clusters are assigned to one of the existing new/old seeds.
  • AIS-Clus: AIS-Clus is an adaptive algorithm which uses the strength of the Artificial Immune System meta-heuristic. Particularly, this algorithm uses the clonal selection theory to adapt clusters for the novel arriving textual streams and the negative selection process to detect novel concepts. AIS-Clus is a density based algorithm which can effectively handle the multi-class detection in the streaming scenario.

    • References

    Data stream clustering Wikipedia
    (Text) CC BY-SA


    Similar Topics