 | ||
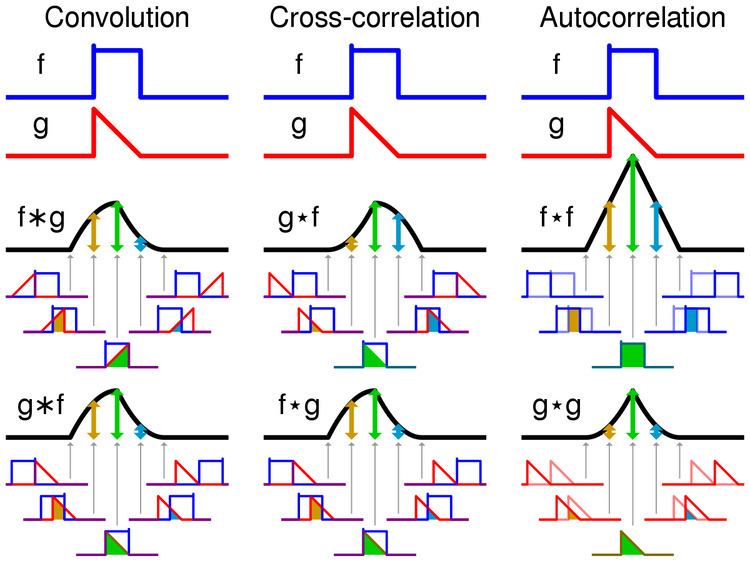
In signal processing, cross-correlation is a measure of similarity of two series as a function of the displacement of one relative to the other. This is also known as a sliding dot product or sliding inner-product. It is commonly used for searching a long signal for a shorter, known feature. It has applications in pattern recognition, single particle analysis, electron tomography, averaging, cryptanalysis, and neurophysiology.
Contents
- Explanation
- Properties
- Time series analysis
- Time delay analysis
- Normalized cross correlation
- Nonlinear systems
- References
For continuous functions f and g, the cross-correlation is defined as:
where
Similarly, for discrete functions, the cross-correlation is defined as:
The cross-correlation is similar in nature to the convolution of two functions.
In an autocorrelation, which is the cross-correlation of a signal with itself, there will always be a peak at a lag of zero, and its size will be the signal power.
In probability and statistics, the term cross-correlations is used for referring to the correlations between the entries of two random vectors X and Y, while the correlations of a random vector X are considered to be the correlations between the entries of X itself, those forming the correlation matrix (matrix of correlations) of X. If each of X and Y is a scalar random variable which is realized repeatedly in temporal sequence (a time series), then the correlations of the various temporal instances of X are known as autocorrelations of X, and the cross-correlations of X with Y across time are temporal cross-correlations.
Furthermore, in probability and statistics the definition of correlation always includes a standardising factor in such a way that correlations have values between −1 and +1.
If
Explanation
As an example, consider two real valued functions
With complex-valued functions
In econometrics, lagged cross-correlation is sometimes referred to as cross-autocorrelation.
Properties
Time series analysis
In time series analysis, as applied in statistics, the cross-correlation between two time series is the normalized cross-covariance function.
Let
where
The cross-correlation of a pair of jointly wide sense stationary stochastic processes can be estimated by averaging the product of samples measured from one process and samples measured from the other (and its time shifts). The samples included in the average can be an arbitrary subset of all the samples in the signal (e.g., samples within a finite time window or a sub-sampling of one of the signals). For a large number of samples, the average converges to the true cross-correlation.
Time delay analysis
Cross-correlations are useful for determining the time delay between two signals, e.g. for determining time delays for the propagation of acoustic signals across a microphone array. After calculating the cross-correlation between the two signals, the maximum (or minimum if the signals are negatively correlated) of the cross-correlation function indicates the point in time where the signals are best aligned, i.e. the time delay between the two signals is determined by the argument of the maximum, or arg max of the cross-correlation, as in
Normalized cross-correlation
For image-processing applications in which the brightness of the image and template can vary due to lighting and exposure conditions, the images can be first normalized. This is typically done at every step by subtracting the mean and dividing by the standard deviation. That is, the cross-correlation of a template,
where
and
then the above sum is equal to
where
Normalized correlation is one of the methods used for template matching, a process used for finding incidences of a pattern or object within an image. It is also the 2-dimensional version of Pearson product-moment correlation coefficient.
Nonlinear systems
Caution must be applied when using cross correlation for nonlinear systems. In certain circumstances, which depend on the properties of the input, cross correlation between the input and output of a system with nonlinear dynamics can be completely blind to certain nonlinear effects. This problem arises because some quadratic moments can equal zero and this can incorrectly suggest that there is little "correlation" (in the sense of statistical dependence) between two signals, when in fact the two signals are strongly related by nonlinear dynamics.
