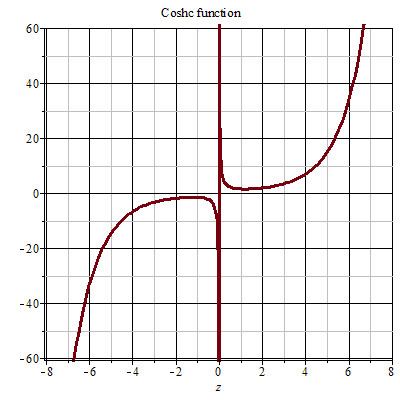
In mathematics, the Coshc function appears frequently in papers about optical scattering, Heisenberg Spacetime and hyperbolic geometry. It is defined as
Coshc
(
z
)
=
cosh
(
z
)
z
It is a solution of the following differential equation:
w
(
z
)
z
−
2
d
d
z
w
(
z
)
−
z
d
2
d
z
2
w
(
z
)
=
0
Imaginary part in complex plane
Im
(
cosh
(
x
+
i
y
)
x
+
i
y
)
Real part in complex plane
Re
(
cosh
(
x
+
i
y
)
x
+
i
y
)
absolute magnitude
|
cosh
(
x
+
i
y
)
x
+
i
y
|
First-order derivative
1
−
cosh
(
z
)
)
2
z
−
cosh
(
z
)
z
2
Real part of derivative
−
Re
(
−
1
−
(
cosh
(
x
+
i
y
)
)
2
x
+
i
y
+
cosh
(
x
+
i
y
)
(
x
+
i
y
)
2
)
Imaginary part of derivative
−
Im
(
−
1
−
(
cosh
(
x
+
i
y
)
)
2
x
+
i
y
+
cosh
(
x
+
i
y
)
(
x
+
i
y
)
2
)
absolute value of derivative
|
−
1
−
(
cosh
(
x
+
i
y
)
)
2
x
+
i
y
+
cosh
(
x
+
i
y
)
(
x
+
i
y
)
2
|