 | ||
Control reconfiguration is an active approach in control theory to achieve fault-tolerant control for dynamic systems. It is used when severe faults, such as actuator or sensor outages, cause a break-up of the control loop, which must be restructured to prevent failure at the system level. In addition to loop restructuring, the controller parameters must be adjusted to accommodate changed plant dynamics. Control reconfiguration is a building block toward increasing the dependability of systems under feedback control.
Contents
- Control reconfiguration by arh eih hena francisco
- Fault modelling
- Reconfiguration goals
- Fault hiding
- Linear model following
- Optimisation based control schemes
- Probabilistic approaches
- Learning control
- Mathematical tools and frameworks
- References
Control reconfiguration by arh eih hena francisco
Fault modelling
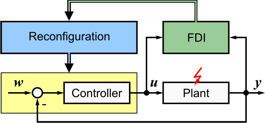
The figure to the right shows a plant controlled by a controller in a standard control loop.
The nominal linear model of the plant is
The plant subject to a fault (indicated by a red arrow in the figure) is modelled in general by
where the subscript
The upper part of the figure shows a supervisory loop consisting of fault detection and isolation (FDI) and reconfiguration which changes the loop by
- choosing new input and output signals from {
u , y } to reach the control goal, - changing the controller internals (including dynamic structure and parameters),
- adjusting the reference input
w .
To this end, the vectors of inputs and outputs contain all available signals, not just those used by the controller in fault-free operation.
Alternative scenarios can model faults as an additive external signal
Reconfiguration goals
The goal of reconfiguration is to keep the reconfigured control-loop performance sufficient for preventing plant shutdown. The following goals are distinguished:
- Stabilization
- Equilibrium recovery
- Output trajectory recovery
- State trajectory recovery
- Transient time response recovery
Internal stability of the reconfigured closed loop is usually the minimum requirement. The equilibrium recovery goal (also referred to as weak goal) refers to the steady-state output equilibrium which the reconfigured loop reaches after a given constant input. This equilibrium must equal the nominal equilibrium under the same input (as time tends to infinity). This goal ensures steady-state reference tracking after reconfiguration. The output trajectory recovery goal (also referred to as strong goal) is even stricter. It requires that the dynamic response to an input must equal the nominal response at all times. Further restrictions are imposed by the state trajectory recovery goal, which requires that the state trajectory be restored to the nominal case by the reconfiguration under any input.
Usually a combination of goals is pursued in practice, such as the equilibrium-recovery goal with stability.
The question whether or not these or similar goals can be reached for specific faults is addressed by reconfigurability analysis.
Fault hiding
This paradigm aims at keeping the nominal controller in the loop. To this end, a reconfiguration block can be placed between the faulty plant and the nominal controller. Together with the faulty plant, it forms the reconfigured plant. The reconfiguration block has to fulfill the requirement that the behaviour of the reconfigured plant matches the behaviour of the nominal, that is fault-free plant.
Linear model following
In linear model following, a formal feature of the nominal closed loop is attempted to be recovered. In the classical pseudo-inverse method, the closed loop system matrix
In perfect model following, a dynamic compensator is introduced to allow for the exact recovery of the complete loop behaviour under certain conditions.
In eigenstructure assignment, the nominal closed loop eigenvalues and eigenvectors (the eigenstructure) is recovered to the nominal case after a fault.
Optimisation-based control schemes
Optimisation control schemes include: linear-quadratic regulator design (LQR), model predictive control (MPC) and eigenstructure assignment methods.
Probabilistic approaches
Some probabilistic approaches have been developed.
Learning control
There are learning automata, neural networks, etc.
Mathematical tools and frameworks
The methods by which reconfiguration is achieved differ considerably. The following list gives an overview of mathematical approaches that are commonly used.
