Conformal geometric algebra

Notation and terminology

The Euclidean space containing the objects being modelled is referred to here as the base space, and the algebraic space used to projectively model these objects is referred to here as the representation space. A homogeneous subspace refers to a linear subspace of the algebraic space.

The terms for objects: point, line, circle, sphere, quasi-sphere etc. are used to mean either the geometric object in the base space, or the homogeneous subspace of the representation space that represents that object, with the latter generally being intended unless indicated otherwise. Algebraically, any nonzero null element of the homogeneous subspace will be used, with one element being referred to as normalized by some criterion.

Boldface lowercase Latin letters are used to represent position vectors from the origin to a point in the base space. Italic symbols are used for other elements of the representation space.

Base and representation spaces

The base space E^p,q is represented by extending a basis for the displacements from a chosen origin and adding two basis vectors e₋ and e₊ orthogonal to the base space and to each other, with e₋² = −1 and e₊² = +1, creating the representation space ℝ^p+1,q+1.

It is convenient to use two null vectors n_o and n_∞ as basis vectors in place of e₊ and e₋, where n_o = (e₋ − e₊)/2, and n_∞ = e₋ + e₊. It can be verified, where x is in the base space, that:

n o 2 = 0 n o ⋅ n ∞ = − 1 n o ⋅ x = 0 n ∞ 2 = 0 n o ∧ n ∞ = e − e + n ∞ ⋅ x = 0

These properties lead to the following formulas for the basis vector coefficients of a general vector r in the representation space for a basis with elements e_i orthogonal to every other basis element:

The coefficient of n_o for r is −n_∞ ⋅ rThe coefficient of n_∞ for r is −n_o ⋅ rThe coefficient of e_i for r is e_i⁻¹ ⋅ r.

Mapping between the base space and the representation space

The mapping from a vector in the base space (being from the origin to a point in the affine space represented) is given by the formula:

F : x ↦ n o + x + 1 2 x 2 n ∞

Points and other objects that differ only by a nonzero scalar factor all map to the same object in the base space. When normalisation is desired, as for generating a simple reverse map of a point from the representation space to the base space or determining distances, the condition F(x) ⋅ n_∞ = −1 may be used.

The forward mapping is equivalent to:

first conformally projecting x from e₁₂₃ onto a unit 3-sphere in the space e₊ ∧ e₁₂₃ (in 5-D this is in the subspace r ⋅ (−n_o − 1/2n_∞) = 0);

then lift this into a projective space, by adjoining e_– = 1, and identifying all points on the same ray from the origin (in 5-D this is in the subspace r ⋅ (−n_o − 1/2n_∞) = 1);

then change the normalisation, so the plane for the homogeneous projection is given by the n_o co-ordinate having a value 1, i.e. r ⋅ n_∞ = −1.

Inverse mapping

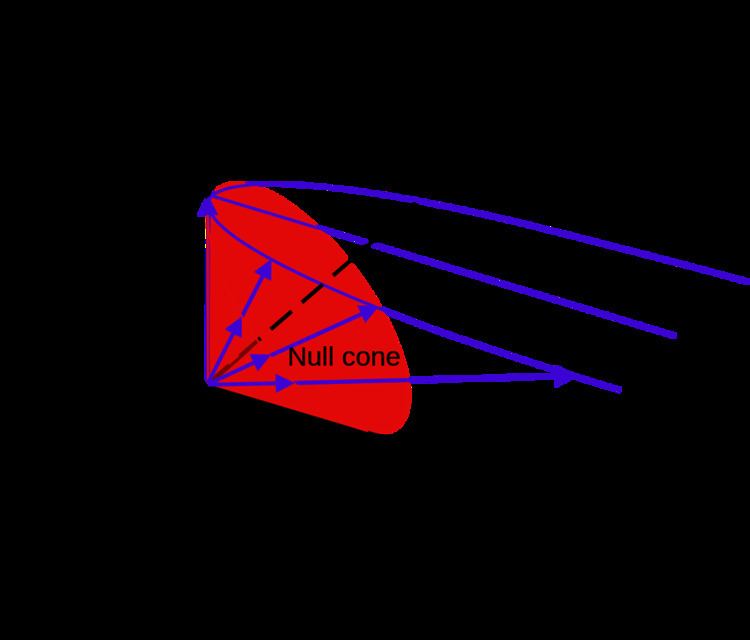
An inverse mapping for X on the null cone is given (Perwass eqn 4.37) by

X ↦ P n ∞ ∧ n o ⊥ ( X − X ⋅ n ∞ )

This first gives a stereographic projection from the light-cone onto the plane r ⋅ n_∞ = −1, and then throws away the n_o and n_∞ parts, so that the overall result is to map all of the equivalent points αX = α(n_o + x + 1/2x²n_∞) to x.

Origin and point at infinity

The point x = 0 in ℝ^p,q maps to n_o in ℝ^p+1,q+1, so n_o is identified as the (representation) vector of the point at the origin.

A vector in ℝ^p+1,q+1 with a nonzero n_∞ coefficient, but a zero n_o coefficient, must (considering the inverse map) be the image of an infinite vector in ℝ^p,q. The direction n_∞ therefore represents the (conformal) point at infinity. This motivates the subscripts _o and _∞ for identifying the null basis vectors.

The choice of the origin is arbitrary: any other point may be chosen, as the representation is of an affine space. The origin merely represents a reference point, and is algebraically equivalent to any other point. Changing the origin corresponds to a rotation in the representation space.

As the solution of a pair of equations

Given any nonzero blade A of the representing space, the set of vectors that are solutions to a pair of homogeneous equations of the form

X 2 = 0 X ∧ A = 0

is the union of homogeneous 1-d subspaces of null vectors, and is thus a representation of a set of points in the base space. This leads to the choice of a blade A as being a useful way to represent a particular class of geometric object. Specific cases for the blade A (independent of the number of dimensions of the space) when the base space is Euclidean space are:

a scalar: the empty set

a vector: a single point

a bivector: a pair of points

a trivector: a generalized circle

a 4-vector: a generalized sphere

etc.

These each may split into three cases according to whether A² is positive, zero or negative, corresponding (in reversed order in some cases) to the object as listed, a degenerate case of a single point, or no points (where the nonzero solutions of X ∧ A exclude null vectors).

The listed geometric objects (generalized n-spheres) become quasi-spheres in the more general case of the base space being pseudo-Euclidean.

Flat objects may be identified by the point at infinity being included in the solutions. Thus, if n_∞ ∧ A = 0, the object will be a line, plane, etc., for the blade A respectively being of grade 3, 4, etc.

As derived from points of the object

A blade A representing of one of this class of object may be found as the outer product of linearly independent vectors representing points on the object. In the base space, this linear independence manifests as each point lying outside the object defined by the other points. So, for example, a fourth point lying on the generalized circle defined by three distinct points cannot be used as a fourth point to define a sphere.

odds

Points in e₁₂₃ map onto the null cone—the null parabola if we set r . n_∞ = -1.We can consider the locus of points in e₁₂₃ s.t. in conformal space g(x) . A = 0, for various types of geometrical object A.We start by observing that g ( a ) . g ( b ) = − 1 2 ∥ a − b ∥ 2

compare:

x. a = 0 => x perp a; x.(a∧b) = 0 => x perp a and x perp b

x∧a = 0 => x parallel to a; x∧(a∧b) = 0 => x parallel to a or to b (or to some linear combination)

the inner product and outer product representations are related by dualisation

x∧A = 0 <=> x . A* = 0 (check—works if x is 1-dim, A is n-1 dim)

g(x) . A = 0

A point: the locus of x in R³ is a point if A in R^4,1 is a vector on the null cone.

A sphere: the locus of x is a sphere if A = S, a vector off the null cone.

A plane: the locus of x is a plane if A = P, a vector with a zero n_o component. In a homogeneous projective space such a vector P represents a vector on the plane n_o=1 that would be infinitely far from the origin (ie infinitely far outside the null cone) , so g(x).P =0 corresponds to x on a sphere of infinite radius, a plane.

In particular:

P = a ^ + α e ∞ corresponds to x on a plane with normal a ^ an orthogonal distance α from the origin.

P = g ( a ) − g ( b ) corresponds to a plane half way between a and b, with normal a - b

circles

tangent planes

lines

lines at infinity

point pairs

Transformations

reflections

It can be verified that forming P g(x) P gives a new direction on the null-cone, g(x' ), where x' corresponds to a reflection in the plane of points p in R³ that satisfy g(p) . P = 0.g(x) . A = 0 => P g(x) . A P = 0 => P g(x) P . P A P (and similarly for the wedge product), so the effect of applying P sandwich-fashion to any the quantities A in the section above is similarly to reflect the corresponding locus of points x, so the corresponding circles, spheres, lines and planes corresponding to particular types of A are reflected in exactly the same way that applying P to g(x) reflects a point x.

This reflection operation can be used to build up general translations and rotations:

translations

Reflection in two parallel planes gives a translation, g ( x ′ ) = P β P α g ( x ) P α P β If P α = a ^ + α e ∞ and P β = a ^ + β e ∞ then x ′ = x + 2 ( β − α ) a ^

rotations

g ( x ′ ) = b ^ a ^ g ( x ) a ^ b ^ corresponds to an x' that is rotated about the origin by an angle 2 θ where θ is the angle between a and b -- the same effect that this rotor would have if applied directly to x.

general rotations

rotations about a general point can be achieved by first translating the point to the origin, then rotating around the origin, then translating the point back to its original position, i.e. a sandwiching by the operator T R T ~ so g ( G x ) = T R T ~ g ( x ) T R ~ T ~

screws

the effect a screw, or motor, (a rotation about a general point, followed by a translation parallel to the axis of rotation) can be achieved by sandwiching g(x) by the operator M = T 2 T 1 R T 1 ~ .M can also be parametrised M = T ′ R ′ (Chasles' theorem)

inversions

an inversion is a reflection in a sphere – various operations that can be achieved using such inversions are discussed at inversive geometry. In particular, the combination of inversion together with the Euclidean transformations translation and rotation is sufficient to express any conformal mapping – i.e. any mapping that universally preserves angles. (Liouville's theorem).

dilations

two inversions with the same centre produce a dilation.