 | ||
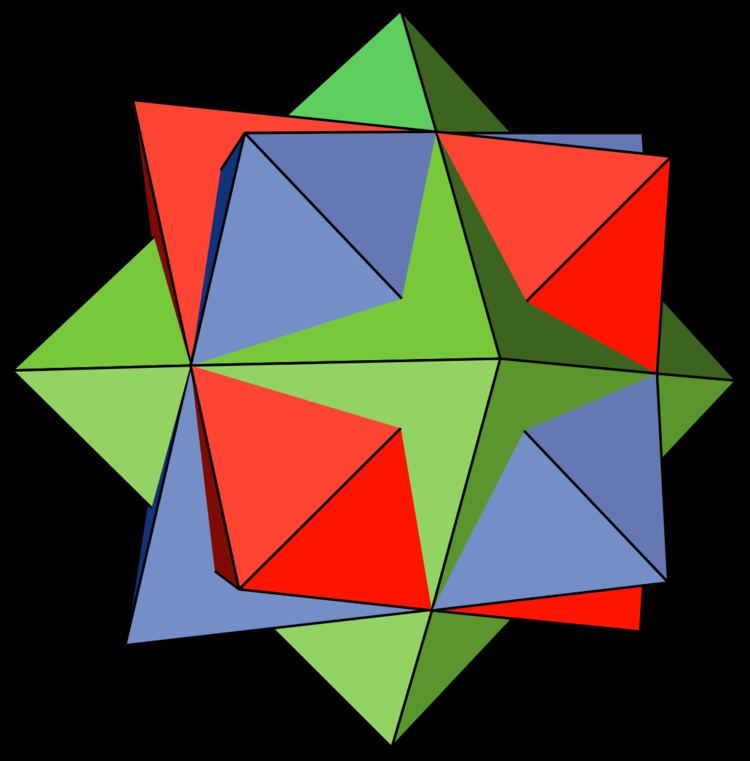
In mathematics, the compound of three octahedra or octahedron 3-compound is a polyhedral compound formed from three regular octahedra, all sharing a common center but rotated with respect to each other. Although appearing earlier in the mathematical literature, it was rediscovered and popularized by M. C. Escher, who used it in the central image of his 1948 woodcut Stars.
Contents
Construction
A regular octahedron can be circumscribed around a cube in such a way that the eight edges of two opposite squares of the cube lie on the eight faces of the octahedron. The three octahedra formed in this way from the three pairs of opposite cube squares form the compound of three octahedra. The eight cube vertices are the same as the eight points in the compound where three edges cross each other. Each of the octahedron edges that participates in these triple crossings is divided by the crossing point in the ratio 1:√2. The remaining octahedron edges cross each other in pairs, within the interior of the compound; their crossings are at their midpoints and form right angles.
The compound of three octahedra can also be formed from three copies of a single octahedron by rotating each copy by an angle of π/4 around one of the three symmetry axes that pass through two opposite vertices of the starting octahedron. A third construction for the same compound of three octahedra is as the dual polyhedron of the compound of three cubes, one of the uniform polyhedron compounds.
The six vertices of one of the three octahedra may be given by the coordinates (0, 0, ±2) and (±√2, ±√2, 0). The other two octahedra have coordinates that may be obtained from these coordinates by exchanging the z coordinate for the x or y coordinate.
Symmetries
The compound of three octahedra has the same symmetry group as a single octahedron. It is an isohedral deltahedron, meaning that its faces are equilateral triangles and that it has a symmetry taking every face to every other face. There is one known infinite family of isohedral deltahedra, and 36 more that do not fall into this family; the compound of three octahedra is one of the 36 sporadic examples. However, its symmetry group does not take every vertex to every other vertex, so it is not itself a uniform polyhedron compound.
The intersection of the three octahedra is a convex polyhedron with 14 vertices and 24 faces, a tetrakis hexahedron, formed by attaching a low square pyramid to each face of the central cube. Thus, the compound can be seen as a stellation of the tetrakis hexahedron. A different form of the tetrakis hexahedron, formed by using taller pyramids on each face of the cube, is non-convex but has equilateral triangle faces that again lie on the same planes as the faces of the three octahedra; it is another of the known isohedral deltahedra. A third isohedral deltahedron sharing the same face planes, the compound of six tetrahedra, may be formed by stellating each face of the compound of three octahedra to form three stellae octangulae. A fourth isohedral deltahedron with the same face planes, also a stellation of the compound of three octahedra, has the same combinatorial structure as the tetrakis hexahedron but with the cube faces dented inwards into intersecting pyramids rather than attaching the pyramids to the exterior of the cube.
The cube around which the three octahedra can be circumscribed has nine planes of reflection symmetry. Three of these reflection panes pass parallel to the sides of the cube, halfway between two opposite sides; the other six pass diagonally across the cube, through four of its vertices. These nine planes coincide with the nine equatorial planes of the three octahedra.
History
In the 15th-century manuscript Libellus De Quinque Corporibus Regularibus by Piero della Francesca, della Francesca already includes a drawing of an octahedron circumscribed around a cube, with eight of the cube edges lying in the octahedron's eight faces. Three octahedra circumscribed in this way around a single cube would form the compound of three octahedra, but della Francesca does not depict the compound.
The next appearance of the compound of three octahedra in the mathematical literature appears to be a 1900 work by Max Brückner, which mentions it and includes a photograph of a model of it.
Dutch artist M. C. Escher, in his 1948 woodcut Stars, used as the central figure of the woodcut a cage in this shape, containing two chameleons and floating through space. Escher would not have been familiar with Brückner's work and H. S. M. Coxeter writes that "It is remarkable that Escher, without any knowledge of algebra or analytic geometry, was able to rediscover this highly symmetrical figure." Earlier in 1948, Escher had made a preliminary woodcut with a similar theme, Study for Stars, but instead of using the compound of three regular octahedra in the study he used a different but related shape, a stellated rhombic dodecahedron (sometimes called Escher's solid), which can be formed as a compound of three flattened octahedra. This form as a polyhedron is topologically identical to the disdyakis dodecahedron, which can be seen as rhombic dodecahedron with shorter pyramids on the rhombic faces. The dual figure of the octahedral compound, the compound of three cubes, is also shown in a later Escher woodcut, Waterfall, next to the same stellated rhombic dodecahedron.
The compound of three octahedra re-entered the mathematical literature more properly with the work of Bakos & Johnson (1959), who observed its existence and provided coordinates for its vertices. It was studied in more detail by Wenninger (1968) and Coxeter (1985).
Other compounds of three octahedra
With the octahedra seen as triangular antiprisms, another uniform prismatic compound of antiprisms exists with D3d symmetry, order 12. Each antiprism is rotated 40 degrees. The top and bottom planes can be seen to contain the compound enneagram, {9/3} or 3{3}.
