Complexity index

Definition of sentry function

For a concept class C on a space X , a sentry function is a total function S : C ∪ { ∅ , X } ↦ 2 X satisfying the following conditions:

1. Sentinels are outside the sentineled concept ( c ∩ S ( c ) = ∅ for all c ∈ C ).
2. Sentinels are inside the invading concept (Having introduced the sets c + = c ∪ S ( c ) , an invading concept c ′ ∈ C is such that c ′ ⊈ c and c + ⊆ ( c ′ ) + . Denoting u p ( c ) the set of concepts invading c, we must have that if c 2 ∈ u p ( c 1 ) , then c 2 ∩ S ( c 1 ) ≠ ∅ ).
3. S ( c ) is a minimal set with the above properties (No S ′ ≠ S exists satisfying (1) and (2) and having the property that S ′ ( c ) ⊆ S ( c ) for every c ∈ C ).
4. Sentinels are honest guardians. It may be that c ⊆ ( c ′ ) + but S ( c ) ∩ c ′ = ∅ so that c ′ ∉ u p ( c ) . This however must be a consequence of the fact that all points of S ( c ) are involved in really sentineling c against other concepts in u p ( c ) and not just in avoiding inclusion of c + by ( c ′ ) + . Thus if we remove c ′ , S ( c ) remains unchanged (Whenever c 1 and c 2 are such that c 1 ⊂ c 2 ∪ S ( c 2 ) and c 2 ∩ S ( c 1 ) = ∅ , then the restriction of S to { c 1 } ∪ u p ( c 1 ) − { c 2 } is a sentry function on this set).

S ( c ) is the frontier of c upon S .

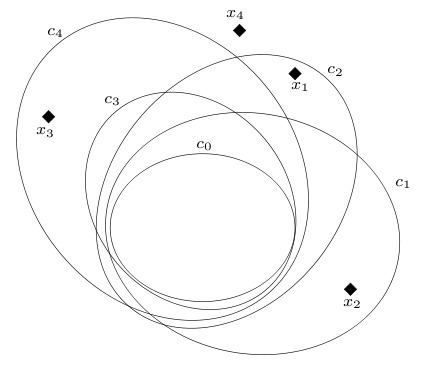
With reference to the picture on the right, { x 1 , x 2 , x 3 } is a candidate frontier of c 0 against c 1 , c 2 , c 3 , c 4 . All points are in the gap between a c i and c 0 . They avoid inclusion of c 0 ∪ { x 1 , x 2 , x 3 } in c 3 , provided that these points are not used by the latter for sentineling itself against other concepts. Vice versa we expect that c 1 uses x 1 and x 3 as its own sentinels, c 2 uses x 2 and x 3 and c 4 uses x 1 and x 2 analogously. Point x 4 is not allowed as a c 0 sentry point since, like any diplomatic seat, it should be located outside all other concepts just to ensure that it is not occupied in case of invasion by c 0 .

Definition of detail

The frontier size of the most expensive concept to be sentineled with the least efficient sentineling function, i.e. the quantity

is called detail of C . S spans also over sentry functions on subsets of X sentineling in this case the intersections of the concepts with these subsets. Actually, proper subsets of X may host sentineling tasks that prove harder than those emerging with X itself.

The detail D C is a complexity measure of concept classes dual to the VC dimension D V C . The former uses points to separate sets of concepts, the latter concepts for partitioning sets of points. In particular the following inequality holds (Apolloni 1997)

See also Rademacher complexity for a recently introduced class complexity index.

Example: continuous spaces

Class C of circles in R 2 has detail D C = 2 , as shown in the picture on left below. Similarly, for the class of segments on R , as shown in the picture on right.

Example: discrete spaces

The class C = { c 1 , c 2 , c 3 , c 4 } on X = { x 1 , x 2 , x 3 } whose concepts are illustrated in the following scheme, where “+” denotes an element x j belonging to c i , “-” an element outside c i and a sentry point:

This class has D C = 2 . As usual we may have different sentineling functions. A worst case S, as illustrated, is: S ( c 1 ) = { x 1 , x 2 } , S ( c 2 ) = { x 1 } , S ( c 3 ) = { x 2 } , S ( c 4 ) = ∅ . However a cheaper one is S ( c 1 ) = { x 3 } , S ( c 2 ) = { x 1 } , S ( c 3 ) = { x 2 } , S ( c 4 ) = ∅ :