Color difference - Alchetron, The Free Social Encyclopedia

The difference or distance between two colors is a metric of interest in color science. It allows quantified examination of a notion that formerly could only be described with adjectives. Quantification of these properties is of great importance to those whose work is color critical. Common definitions make use of the Euclidean distance in a device independent color space.

Euclidean

As most definitions of color distance are distances within a color space, the standard means of determining distances is the Euclidean distance. If one presently has an RGB (Red, Green, Blue) tuple and wishes to find the color difference, computationally one of the easiest is to call R, G, B linear dimensions defining the color space.

d i s t a n c e = ( R 2 − R 1 ) 2 + ( G 2 − G 1 ) 2 + ( B 2 − B 1 ) 2

When the result should be both computationally simple as well, it is often acceptable to remove the square root and simply use:

d i s t a n c e 2 = ( R 2 − R 1 ) 2 + ( G 2 − G 1 ) 2 + ( B 2 − B 1 ) 2

This is will work in cases when a single color is to be compared to a single color and the need is to simply know whether a distance is further, but if the color distances are summed up such a metric effectively becomes the variance of the color distances.

There have been many attempts to weight RGB values to better fit human perception commonly 30%, 59%, 11% however these are demonstratively worse at color determinations and are properly the contributions to brightness of these colors, rather than the degree to which human vision has less tolerance for these colors The closer approximations would be properly, 2,4,3 2 × Δ R 2 + 4 × Δ G 2 + 3 × Δ B 2 One of the better low-cost approximations,

r ¯ = C 1 , R + C 2 , R 2 Δ R = C 1 , R − C 2 , R Δ G = C 1 , G − C 2 , G Δ B = C 1 , B − C 2 , B Δ C = ( 2 + r ¯ 256 ) × Δ R 2 + 4 × Δ G 2 + ( 2 + 255 − r ¯ 256 ) × Δ B 2

There are a number of color distance formulae that attempt to use color spaces like HSV with the hue as a circle, placing the various colors within a three dimensional space of either a cylinder or cone, but most of these are just modifications of RGB without accounting for differences in human color perception they will tend to be on par with a simple Euclidean metric.

LAB Delta E

The International Commission on Illumination (CIE) calls their distance metric ΔE^*_ab (also called ΔE*, dE*, dE, or "Delta E") where delta is a Greek letter often used to denote difference, and E stands for Empfindung; German for "sensation". Use of this term can be traced back to the influential Hermann von Helmholtz and Ewald Hering.

Different studies have proposed different ΔE values that have a JND (just noticeable difference). Unempirically, a value of '1.0' is often mentioned, but in a recent study, Mahy et al. (1994) assessed a JND of 2.3 ΔE. However, perceptual non-uniformities in the underlying CIELAB color space prevent this and have led to the CIE's refining their definition over the years, leading to the superior (as recommended by the CIE) 1994 and 2000 formulas. These non-uniformities are important because the human eye is more sensitive to certain colors than others. A good metric should take this into account in order for the notion of a "just noticeable difference" to have meaning. Otherwise, a certain ΔE that may be insignificant between two colors that the eye is insensitive to may be conspicuous in another part of the spectrum.

CIE76

The 1976 formula is the first color-difference formula that related a measured to a known set of CIELAB coordinates. This formula has been succeeded by the 1994 and 2000 formulas because the CIELAB space turned out to be not as perceptually uniform as intended, especially in the saturated regions. This means that this formula rates these colors too highly as opposed to other colors.

Using ( L 1 ∗ , a 1 ∗ , b 1 ∗ ) and ( L 2 ∗ , a 2 ∗ , b 2 ∗ ) , two colors in L*a*b*:

Δ E a b ∗ = ( L 2 ∗ − L 1 ∗ ) 2 + ( a 2 ∗ − a 1 ∗ ) 2 + ( b 2 ∗ − b 1 ∗ ) 2

Δ E a b ∗ ≈ 2.3 corresponds to a JND (just noticeable difference).

CIE94

The 1976 definition was extended to address perceptual non-uniformities, while retaining the L*a*b* color space, by the introduction of application-specific weights derived from an automotive paint test's tolerance data.

ΔE (1994) is defined in the L*C*h* color space with differences in lightness, chroma and hue calculated from L*a*b* coordinates. Given a reference color ( L 1 ∗ , a 1 ∗ , b 1 ∗ ) and another color ( L 2 ∗ , a 2 ∗ , b 2 ∗ ) , the difference is:

Δ E 94 ∗ = ( Δ L ∗ k L S L ) 2 + ( Δ C a b ∗ k C S C ) 2 + ( Δ H a b ∗ k H S H ) 2

where:

Δ L ∗ = L 1 ∗ − L 2 ∗ C 1 ∗ = a 1 ∗ 2 + b 1 ∗ 2 C 2 ∗ = a 2 ∗ 2 + b 2 ∗ 2 Δ C a b ∗ = C 1 ∗ − C 2 ∗ Δ H a b ∗ = Δ E a b ∗ 2 − Δ L ∗ 2 − Δ C a b ∗ 2 = Δ a ∗ 2 + Δ b ∗ 2 − Δ C a b ∗ 2 Δ a ∗ = a 1 ∗ − a 2 ∗ Δ b ∗ = b 1 ∗ − b 2 ∗ S L = 1 S C = 1 + K 1 C 1 ∗ S H = 1 + K 2 C 1 ∗

and where k_C and k_H are usually both unity and the weighting factors k_L, K₁ and K₂ depend on the application:

Geometrically, the quantity Δ H a b ∗ corresponds to the arithmetic mean of the chord lengths of the equal chroma circles of the two colors.

CIEDE2000

Since the 1994 definition did not adequately resolve the perceptual uniformity issue, the CIE refined their definition, adding five corrections:

A hue rotation term (R_T), to deal with the problematic blue region (hue angles in the neighborhood of 275°):

Compensation for neutral colors (the primed values in the L*C*h differences)

Compensation for lightness (S_L)

Compensation for chroma (S_C)

Compensation for hue (S_H)

Δ E 00 ∗ = ( Δ L ′ k L S L ) 2 + ( Δ C ′ k C S C ) 2 + ( Δ H ′ k H S H ) 2 + R T Δ C ′ k C S C Δ H ′ k H S H Δ L ′ = L 2 ∗ − L 1 ∗ L ¯ = L 1 ∗ + L 2 ∗ 2 C ¯ = C 1 ∗ + C 2 ∗ 2 a 1 ′ = a 1 ∗ + a 1 ∗ 2 ( 1 − C ¯ 7 C ¯ 7 + 25 7 ) a 2 ′ = a 2 ∗ + a 2 ∗ 2 ( 1 − C ¯ 7 C ¯ 7 + 25 7 ) C ¯ ′ = C 1 ′ + C 2 ′ 2 and Δ C ′ = C 2 ′ − C 1 ′ where C 1 ′ = a 1 ′ 2 + b 1 ∗ 2 C 2 ′ = a 2 ′ 2 + b 2 ∗ 2 h 1 ′ = atan2 ( b 1 ∗ , a 1 ′ ) mod 360 ∘ , h 2 ′ = atan2 ( b 2 ∗ , a 2 ′ ) mod 360 ∘ Note: The inverse tangent (tan⁻¹) can be computed using a common library routine atan2(b, a′) which usually has a range from −π to π radians; color specifications are given in 0 to 360 degrees, so some adjustment is needed. The inverse tangent is indeterminate if both a′ and b are zero (which also means that the corresponding C′ is zero); in that case, set the hue angle to zero. See Sharma 2005, eqn. 7. Δ h ′ = { h 2 ′ − h 1 ′ | h 1 ′ − h 2 ′ | ≤ 180 ∘ h 2 ′ − h 1 ′ + 360 ∘ | h 1 ′ − h 2 ′ | > 180 ∘ , h 2 ′ ≤ h 1 ′ h 2 ′ − h 1 ′ − 360 ∘ | h 1 ′ − h 2 ′ | > 180 ∘ , h 2 ′ > h 1 ′ Note: When either C′₁ or C′₂ is zero, then Δh′ is irrelevant and may be set to zero. See Sharma 2005, eqn. 10. Δ H ′ = 2 C 1 ′ C 2 ′ sin ⁡ ( Δ h ′ / 2 ) , H ¯ ′ = { ( h 1 ′ + h 2 ′ ) / 2 | h 1 ′ − h 2 ′ | ≤ 180 ∘ ( h 1 ′ + h 2 ′ + 360 ∘ ) / 2 | h 1 ′ − h 2 ′ | > 180 ∘ , h 1 ′ + h 2 ′ < 360 ∘ ( h 1 ′ + h 2 ′ − 360 ∘ ) / 2 | h 1 ′ − h 2 ′ | > 180 ∘ , h 1 ′ + h 2 ′ ≥ 360 ∘ Note: When either C′₁ or C′₂ is zero, then H′ is h′₁+h′₂ (no divide by 2; essentially, if one angle is indeterminate, then use the other angle as the average; relies on indeterminate angle being set to zero). See Sharma 2005, eqn. 7 and p. 23 stating most implementations on the internet at the time had "an error in the computation of average hue". T = 1 − 0.17 cos ⁡ ( H ¯ ′ − 30 ∘ ) + 0.24 cos ⁡ ( 2 H ¯ ′ ) + 0.32 cos ⁡ ( 3 H ¯ ′ + 6 ∘ ) − 0.20 cos ⁡ ( 4 H ¯ ′ − 63 ∘ ) S L = 1 + 0.015 ( L ¯ − 50 ) 2 20 + ( L ¯ − 50 ) 2 S C = 1 + 0.045 C ¯ ′ S H = 1 + 0.015 C ¯ ′ T R T = − 2 C ¯ ′ 7 C ¯ ′ 7 + 25 7 sin ⁡ [ 60 ∘ ⋅ exp ⁡ ( − [ H ¯ ′ − 275 ∘ 25 ∘ ] 2 ) ]

CMC l:c (1984)

In 1984, the Colour Measurement Committee of the Society of Dyers and Colourists defined a difference measure, also based on the L*C*h color model. Named after the developing committee, their metric is called CMC l:c. The quasimetric has two parameters: lightness (l) and chroma (c), allowing the users to weight the difference based on the ratio of l:c that is deemed appropriate for the application. Commonly used values are 2:1 for acceptability and 1:1 for the threshold of imperceptibility.

The distance of a color ( L 2 ∗ , C 2 ∗ , h 2 ) to a reference ( L 1 ∗ , C 1 ∗ , h 1 ) is:

Δ E C M C ∗ = ( L 2 ∗ − L 1 ∗ l S L ) 2 + ( C 2 ∗ − C 1 ∗ c S C ) 2 + ( Δ H a b ∗ S H ) 2

S L = { 0.511 L 1 ∗ < 16 0.040975 L 1 ∗ 1 + 0.01765 L 1 ∗ L 1 ∗ ≥ 16 S C = 0.0638 C 1 ∗ 1 + 0.0131 C 1 ∗ + 0.638 S H = S C ( F T + 1 − F )

F = C 1 ∗ 4 C 1 ∗ 4 + 1900 T = { 0.56 + | 0.2 cos ⁡ ( h 1 + 168 ∘ ) | 164 ∘ ≤ h 1 ≤ 345 ∘ 0.36 + | 0.4 cos ⁡ ( h 1 + 35 ∘ ) | otherwise

CMC l:c is designed to be used with D65 and the CIE Supplementary Observer. The formula is not a metric but rather a quasimetric because it violates symmetry, parameter T is based on the hue of the h 1 alone. This reference color means that the color difference from the first color to the second color is different than the color distance from the second color is to the first.

Tolerance

Tolerancing concerns the question "What is a set of colors that are imperceptibly/acceptably close to a given reference?" If the distance measure is perceptually uniform, then the answer is simply "the set of points whose distance to the reference is less than the just-noticeable-difference (JND) threshold." This requires a perceptually uniform metric in order for the threshold to be constant throughout the gamut (range of colors). Otherwise, the threshold will be a function of the reference color—cumbersome as a practical guide.

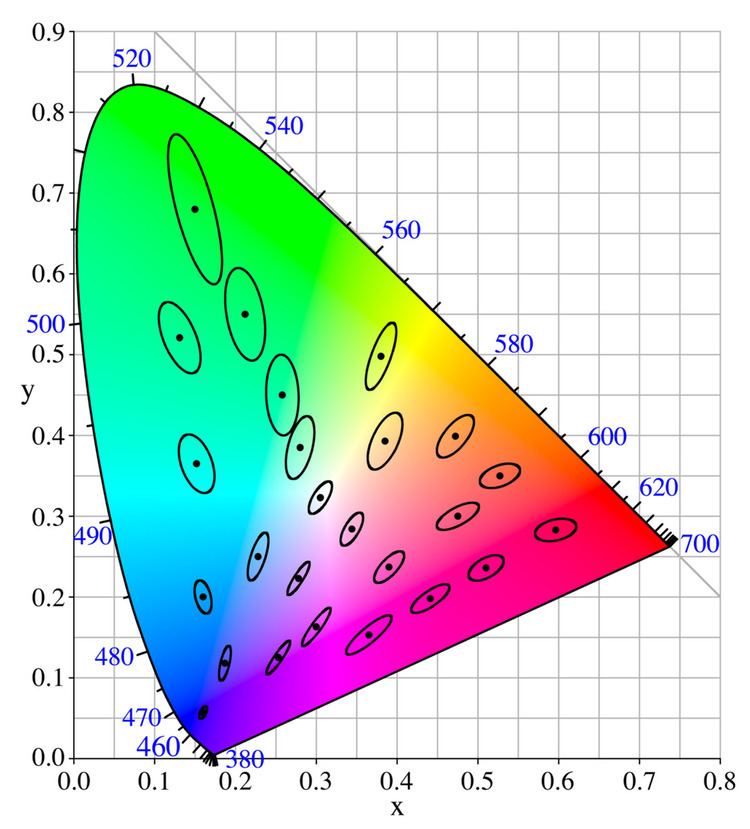
In the CIE 1931 color space, for example, the tolerance contours are defined by the MacAdam ellipse, which holds L* (lightness) fixed. As can be observed on the diagram on the right, the ellipses denoting the tolerance contours vary in size. It is partly this non-uniformity that led to the creation of CIELUV and CIELAB.

More generally, if the lightness is allowed to vary, then we find the tolerance set to be ellipsoidal. Increasing the weighting factor in the aforementioned distance expressions has the effect of increasing the size of the ellipsoid along the respective axis.

References

Color difference Wikipedia

(Text) CC BY-SA

Contents