Clasper (mathematics)

Motivation

Beginning with the Jones polynomial, infinitely many new invariants of knots, links, and 3-manifolds were found during the 1980s. The study of these new `quantum' invariants expanded rapidly into a sub-discipline of low-dimensional topology called quantum topology. A quantum invariant is typically constructed from two ingredients: a formal sum of Jacobi diagrams (which carry a Lie algebra structure), and a representation of a ribbon Hopf algebra such as a quantum group. It is not clear a-priori why either of these ingredients should have anything to do with low-dimensional topology. Thus one of the main problems in quantum topology has been to interpret quantum invariants topologically.

The theory of claspers comes to provide such an interpretation. A clasper, like a framed link, is an embedded topological object in a 3-manifold on which one can perform surgery. In fact, clasper calculus can be thought of as a variant of Kirby calculus on which only certain specific types of framed links are allowed. Claspers may also be interpreted algebraically, as a diagram calculus for the braided strict monoidal category Cob of oriented connected surfaces with connected boundary. Additionally, most crucially, claspers may be roughly viewed as a topological realization of Jacobi diagrams, which are purely combinatorial objects. This explains the Lie algebra structure of the graded vector space of Jacobi diagrams in terms of the Hopf algebra structure of Cob.

Definition

A clasper G = A ∪ B is a compact surface embedded in the interior of a 3-manifold M equipped with a decomposition into two subsurfaces A and B , whose connected components are called the constituents and the edges of G correspondingly. Each edge of G is a band joining two constituents to one another, or joining one constituent to itself. There are four types of constituents: leaves, disk-leaves, nodes, and boxes.

Clasper surgery is most easily defined (after elimination of nodes, boxes, and disk-leaves as described below) as surgery along a link associated to the clasper by replacing each leaf with its core, and replacing each edge by a right Hopf link.

Clasper calculus

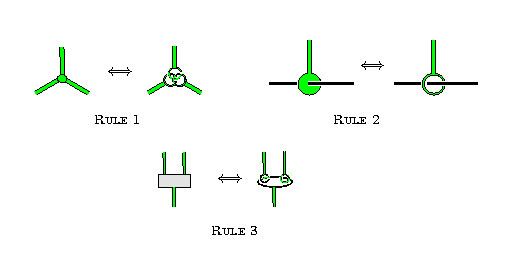
The following are the graphical conventions used when drawing claspers (and may be viewed as a definition for boxes, nodes, and disk-leaves):

Habiro found 12 moves which relate claspers along which surgery gives the same result. These moves form the core of clasper calculus, and give considerable power to the theory as a theorem-proving tool.

Cn-equivalence

Two knots, links, or 3-manifolds are said to be C n -equivalent if they are related by C n -moves, which are the local moves induced by surgeries on a simple tree claspers without boxes or disk-leaves and with n leaves.

For a link L ⊂ M , a C 1 -move is a crossing change. A C 2 -move is a Delta move. Most applications of claspers use only C n -moves.

Main results

For two knots K and K ′ and a non-negative integer k , the following conditions are equivalent:

1. K and K ′ are not distinguished by any invariant of type k .
2. K and K ′ are C k -equivalent.

The corresponding statement is false for links.