 | ||
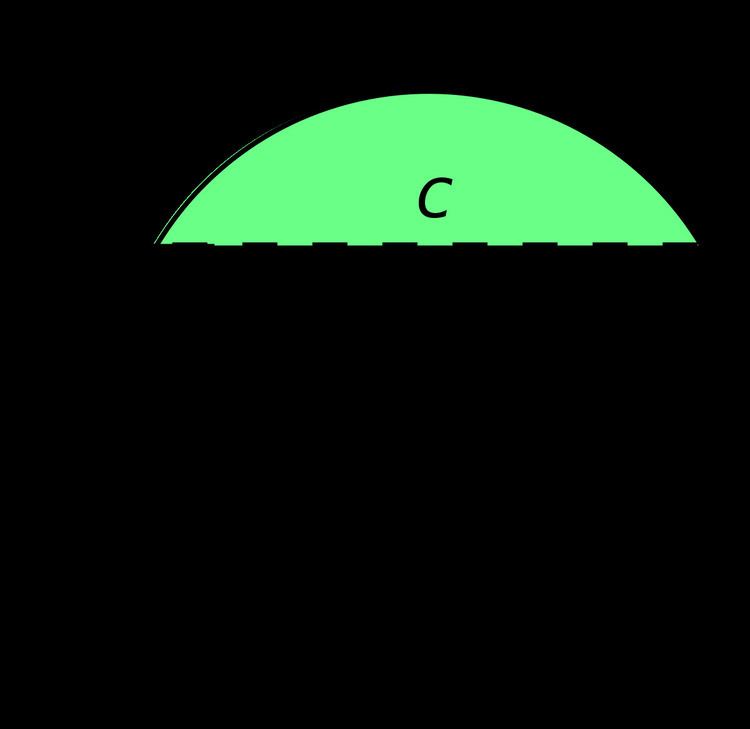
In geometry, a circular segment (symbol: ⌓) is a region of a circle which is "cut off" from the rest of the circle by a secant or a chord. More formally, a circular segment is a region of two-dimensional space that is bounded by an arc (of less than 180°) of a circle and by the chord connecting the endpoints of the arc.
Contents
Formula
Let R be the radius of the circle, θ the central angle in radians, α is the central angle in degrees, c the chord length, s the arc length, h the sagitta (height) of the segment, and d the height of the triangular portion.
The radius is
The radius in terms of h and c can be derived above by using the Intersecting Chords Theorem, where 2R (the diameter) and c are perpendicularly intersecting chords.
The arc length is
The arc length in terms of arcsin can be derived above by considering an inscribed angle that subtends the same arc, and one side of the angle is a diameter. The angle thus inscribed is θ/2 and is part of a right triangle whose hypotenuse is the diameter. This is also useful in deriving some of the trigonometric forms below.
The chord length is
The sagitta is
The angle is
Area
The area A of the circular segment is equal to the area of the circular sector minus the area of the triangular portion—that is,
with the central angle in radians, or
with the central angle in degrees.
Applications
The area formula can be used in calculating the volume of a partially-filled cylindrical tank.
In the design of windows or doors with rounded tops, c and h may be the only known values and can be used to calculate R for the draftsman's compass setting.
