Suvarna Garge (Editor)

Cartesian product of graphs

Updated on
Edit
Like
Comment
Share on FacebookTweet on TwitterShare on LinkedInShare on Reddit
Cartesian product of graphs

In graph theory, the Cartesian product G ◻ H of graphs G and H is a graph such that

Contents

  • the vertex set of G ◻ H is the Cartesian product V(G) × V(H); and
  • any two vertices (u,u') and (v,v') are adjacent in G ◻ H if and only if either
  • u = v and u' is adjacent with v' in H, or
  • u' = v' and u is adjacent with v in G.

    • Cartesian product graphs can be recognized efficiently, in linear time. The operation is commutative as an operation on isomorphism classes of graphs, and more strongly the graphs G ◻ H and H ◻ G are naturally isomorphic, but it is not commutative as an operation on labeled graphs. The operation is also associative, as the graphs (F ◻ G) ◻ H and F ◻ (G ◻ H) are naturally isomorphic.

    The notation G × H is occasionally also used for Cartesian products of graphs, but is more commonly used for another construction known as the tensor product of graphs. The square symbol is the more common and unambiguous notation for the Cartesian product of graphs. It shows visually the four edges resulting from the Cartesian product of two edges.

    Examples

  • The Cartesian product of two edges is a cycle on four vertices: K2 ◻ K2 = C4.
  • The Cartesian product of K2 and a path graph is a ladder graph.
  • The Cartesian product of two path graphs is a grid graph.
  • The Cartesian product of n edges is a hypercube:
    • Thus, the Cartesian product of two hypercube graphs is another hypercube: Qi ◻ Qj = Qi+j.
  • The Cartesian product of two median graphs is another median graph.
  • The graph of vertices and edges of an n-prism is the Cartesian product graph K2 ◻ Cn.
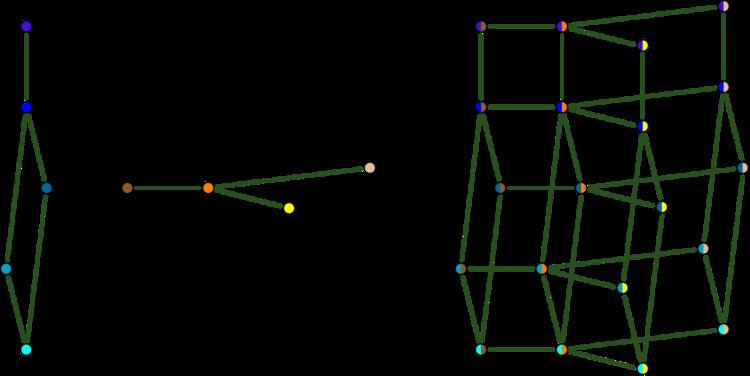
  • The rook's graph is the Cartesian product of two complete graphs.

    • Properties

    If a connected graph is a Cartesian product, it can be factorized uniquely as a product of prime factors, graphs that cannot themselves be decomposed as products of graphs. However, Imrich & Klavžar (2000) describe a disconnected graph that can be expressed in two different ways as a Cartesian product of prime graphs:

    (K1 + K2 + K22) ◻ (K1 + K23) = (K1 + K22 + K24) ◻ (K1 + K2),

    where the plus sign denotes disjoint union and the superscripts denote exponentiation over Cartesian products.

    A Cartesian product is vertex transitive if and only if each of its factors is.

    A Cartesian product is bipartite if and only if each of its factors is. More generally, the chromatic number of the Cartesian product satisfies the equation

    χ(G ◻ H) = max {χ(G), χ(H)}.

    The Hedetniemi conjecture states a related equality for the tensor product of graphs. The independence number of a Cartesian product is not so easily calculated, but as Vizing (1963) showed it satisfies the inequalities

    α(G)α(H) + min{|V(G)|-α(G),|V(H)|-α(H)} ≤ α(G ◻ H) ≤ min{α(G) |V(H)|, α(H) |V(G)|}.

    The Vizing conjecture states that the domination number of a Cartesian product satisfies the inequality

    γ(G ◻ H) ≥ γ(G)γ(H).

    Algebraic graph theory

    Algebraic graph theory can be used to analyse the Cartesian graph product. If the graph G 1 has n 1 vertices and the n 1 × n 1 adjacency matrix A 1 , and the graph G 2 has n 2 vertices and the n 2 × n 2 adjacency matrix A 2 , then the adjacency matrix of the Cartesian product of both graphs is given by

    A 1 ◻ 2 = A 1 ⊗ I n 2 + I n 1 ⊗ A 2 ,

    where ⊗ denotes the Kronecker product of matrices and I n denotes the n × n identity matrix.

    History

    According to Imrich & Klavžar (2000), Cartesian products of graphs were defined in 1912 by Whitehead and Russell. They were repeatedly rediscovered later, notably by Gert Sabidussi (1960).

    References

    Cartesian product of graphs Wikipedia
    (Text) CC BY-SA


    Similar Topics