Vertices 2n Chromatic number 2 | Edges n+2(n-1) Notation Ln | |
 | ||
Chromatic index 3 for n>22 for n=21 for n=1 Properties Unit distanceHamiltonianPlanarBipartite | ||
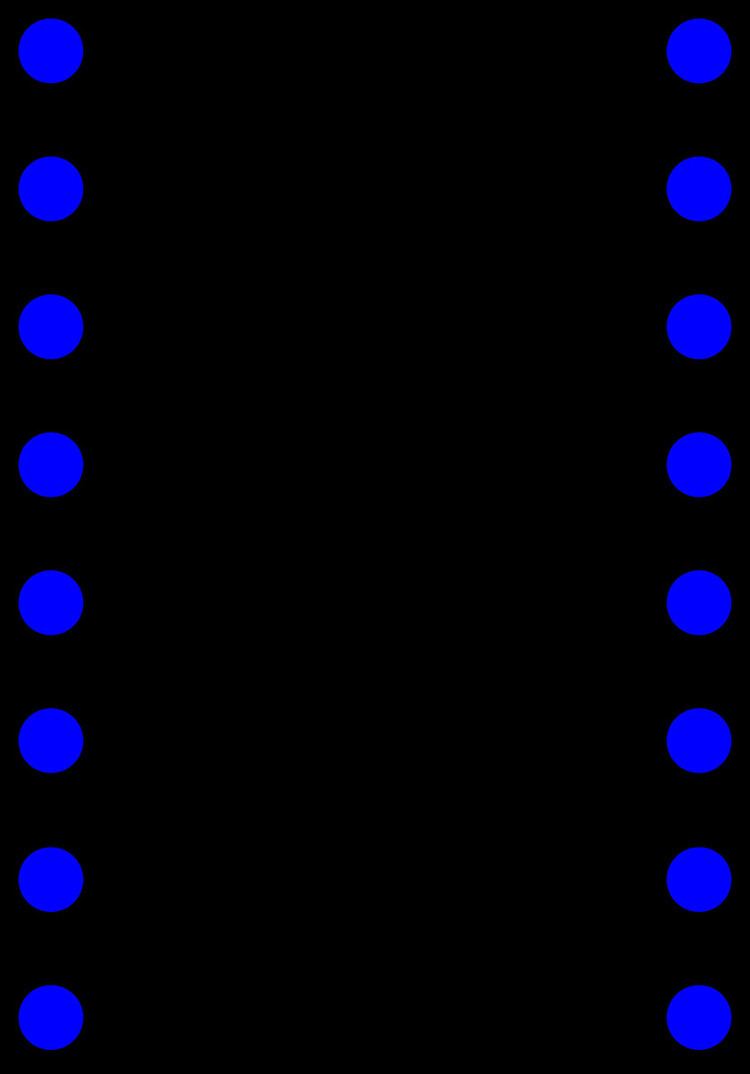
In the mathematical field of graph theory, the ladder graph Ln is a planar undirected graph with 2n vertices and n+2(n-1) edges.
The ladder graph can be obtained as the Cartesian product of two path graphs, one of which has only one edge: Ln,1 = Pn × P1. Adding two more crossed edges connecting the four degree-two vertices of a ladder graph produces a cubic graph, the Möbius ladder.
By construction, the ladder graph Ln is isomorphic to the grid graph G2,n and looks like a ladder with n rungs. It is Hamiltonian with girth 4 (if n>1) and chromatic index 3 (if n>2).
The chromatic number of the ladder graph is 2 and its chromatic polynomial is
Circular ladder graph
The circular ladder graph CLn is the Cartesian product of a cycle of length n≥3 and an edge. In symbols, CLn = Cn × P1. It has 2n nodes and 3n edges. Like the ladder graph, it is connected, planar and Hamiltonian, but it is bipartite if and only if n is even.
