CFD in buildings

Applications

Recently CFD finds very wide application in different areas of science and engineering; some examples are:

In early age of construction, the most of building related issues such as ventilation analysis, wind loading, wind environment etc. were conducted by the wind tunnel tests, but today all these test can be done effectively with CFD technique. CFD technique can resolve all above mentioned issues in very short time period and it is very economical as well as strong approach than the older one (experimental). Recently Computational fluid dynamics is used as a sophisticated airflow modelling method and can be used to predict airflow, heat transfer and contaminant transportation in and around buildings. CFD plays an important role in building design, designing a thermally-conformable, healthy and energy-efficient building. CFD can examine the effectiveness and efficiency of various Heating ventilation and air conditioning (HVAC) systems by easily changing the different types and location of different components of diffuser types and locations, supply air conditions and system control schedules. Furthermore, CFD helps in developing passive heating/cooling/ventilation strategies (e.g. natural ventilation) by modelling and optimizing building site-plans and indoor layouts. Globally building sector shares approximately 40% of total energy consumption.

In present era, there is a huge gap in energy consumption and energy production. As building sector share a huge amount of the total consumption, hence it becomes essential to investigate the optimum configuration for building to reduce the building's share of energy. In order to achieve this, CFD can play an important role. Energy simulation and CFD programs are important building design tools which are used for evaluation of building performance, including thermal comfort, indoor air quality mechanical system efficiency and energy consumption.

CFD in buildings mainly used for one or more followings purposes:

1. Thermal analysis: through walls, roof and floor of buildings
2. Ventilation analysis.
3. Orientation, site and location selection of buildings based on local geographical and environmental conditions.

Thermal analysis

In buildings, heat transfer takes place in its all modes i.e. conduction, convection and radiation. In order to reduce heat losses from buildings, CFD analysis can be done for the optimum configuration of composite walls, roof and floor. The differential form of the general transport equation is as follows:

The numerical solution of above equation can be obtained by finite difference method (FDM), finite volume method (FVM) and finite element method (FEM). In buildings, for heat transfer analysis, the scalar function ф in equation (1) is replaced by Temperature (T), diffusion coefficient Γ is replaced by thermal conductivity k and the source term S ϕ is replaced by heat generation term e or by any heat radiation source Q i or by both (depending upon the nature of source available) and we have different forms of equation for different cases. For simplicity and easy understanding, only 1-Dimensional cases have been discussed.

In buildings the heat transfer analysis can be done for all parts of buildings (walls, roof and floor) in following two ways

1. Steady State Thermal Analysis
2. Transient Thermal Analysis

Steady state thermal analysis

The steady state thermal analysis consist the following type of governing differential equations.

Case-1: General steady state heat conduction equation.

For this case the governing differential equation (GDE) (1) becomes as follows:

Case-2: Steady state heat conduction equation (no heat generation)

For this case the governing differential equation (GDE) (1) becomes as follows:

Case-3: Steady state heat conduction equation (no heat generation and no convection)

For this case the governing differential equation (GDE) (1) becomes as follows:

Transient thermal analysis

The transient thermal analysis consist the following type of governing differential equations.

Case-1: Transient heat conduction

For this case the governing differential equation (GDE) (1) becomes as follows:

Case- 2: Transient heat conduction (no heat generation) For this case the governing differential equation (GDE) (1) becomes as follows:

Case-3: Transient heat conduction (no heat generation and no convection)

For this case the governing differential equation (GDE) (1) becomes as follows:

We can solve these above mentioned governing differential equation (GDE) equations using CFD technique.

Ventilation analysis

The ventilation study in buildings is done to find the thermally comfortable environment with acceptable indoor air quality by regulating indoor air parameters (air temperature, relative humidity, air speed, and chemical species concentrations in the air). CFD finds an important role in regulating the indoor air parameters to predict the ventilation performance in buildings. The ventilation performance prediction provides the information regarding indoor air parameters in a room or a building even before the construction of buildings.

These air parameters are crucial for designing a comfortable indoor as well as outdoor environment. This is because the design of appropriate ventilation systems and the development of control strategies need detailed information regarding the following parameters;

The aforesaid information’s are also useful for an architect to design the building configuration. From the last three decade, the CFD technique is widely used with considerable success in building.

Recently ventilation and its related fields has becomes a great part of wind engineering. A ventilation study can be done using wind tunnel investigation (experimentally) or by CFD modeling (theoretically). Natural ventilation system is always preferred over the forced ventilation system, as it causes to save the burning of fuel, which is economical as well as nature friendly. In present era, due to development of a lot of CFD software and other building's energy simulation software, it becomes quite easy to assess the possibility of natural/forced ventilation system in a building. CFD analysis is quite useful than the experimental approach because here we can find other related relations among the variables in post-processing. The data obtained either experimental or numerically is useful in two ways:

1. better comfort of user.
2. It provides the data which is used as input to the heat balance calculation of the buildings .

Orientation, site and location selection

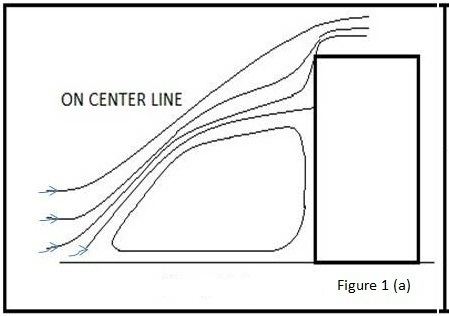
Earlier, the choice of dwelling location was made mindful of the need for water, so most of earlier development started in valley area. In present era, due to advancement in science and technology, it becomes easy to select a proper orientation, site and location of buildings based on local geographical and environmental conditions. In selection of building site and location, wind loading plays and important role. In case of two buildings at a location exists side by side having some gap, when volume of wind blows round the ends of building through the gap is, in first instant the sum of flow around each building separately, then its velocity must increase above that around the end of a single building at the expense of pressure loss.

So, there will be a built of pressure, entering the gap, which will lead to higher wind loads on the sides of buildings. When wind blows over the face of a high rise building, a vortex is created by the downward flow on the front face (as shown in figure-1). The wind speed in the reverse direction near the ground level may have 140 percent of the reference wind speed. So, if any building exist in such region, then that may be subjected to damage (especially the roof of building may get severe damage). Such damage to buildings can be prohibited successfully, if the effects of wind loading are considered in the early stage of construction of a building. In early age of construction all these wind loading effects were determined by the wind tunnel test, but today all these test can be successfully through CFD analysis. The importance of providing pleasant environment to buildings is increasing and architect and wind engineer are often asked to look over the design (orientation, site, location and gaps between the surrounding buildings) in the formative stage of buildings & planning stage of construction. So by using CFD analysis, we can find the suitable information (local wind velocity, convective coefficients, and solar radiation intensity) for orientation, site and location selection of buildings.

CFD approach for heat transfer analysis in buildings

CFD technique can be used for the analysis of heat transfer in each part of a building.CFD technique finds the solution by following ways:

1. Discretization of the governing differential equation using numerical methods (Finite difference method has been discussed).
2. Solve the discretized version of equation with high performance computers.

Discretization of the governing differential equations for the steady state heat transfer analysis

Consider a building having a plane wall with thickness L, heat generation e and constant thermal conductivity k. The wall is subdivided into M equal regions of thickness Δ x = X/T in x-direction, and the divisions between the regions are selected as nodes as shown in figure-2.

The whole domain of wall in x-direction is divided in elements as shown in figure and the size of all interior elements is same while for exterior elements it is half.

Now to obtain the FDM solution for the interior nodes, consider the element represented by the node m which is surrounded by neighboring nodes m-1 and m+1. The FDM technique presumes that temperature varies linearly in walls (shown in figure-3). FDM solution is:( for all interior nodes except to 0 and last node)

Boundary conditions

Above equation is valid only to interior nodes only. To obtain the solution for exterior nodes we have to apply the boundary conditions (as applicable), which are as follows. 1.Specified heat flux boundary condition

When boundary is insulated (q=0)

2. Convective boundary condition

3. Radiation boundary condition

4. Combined convective and radiation boundary condition (shown in figure-4).

or when radiation and convection heat transfer coefficient are combined, above equation becomes as follows;

5. Combined convective, radiation and heat flux boundary condition

6.Interface boundary condition : when there is an interface (in composite walls) of different walls having different thermo-physical properties, the two different solid media A and B are assumed to be perfect contact and thus have same temperature at interface at node m (as shown in figure-5).

In above equations q_0 = denotes specified heat flux is in ( W / m 2 ) , h =convective coefficient, h c o m b i n e d = combined convective and radiation heat transfer coefficient, T s u r = Temperature of surrounding surface, T ( ∞ ) =Ambient Temperature, T 0 = Temperature of at initial node. Note: For interior side of wall we can apply the suitable boundary condition from above (as applicable), in that case T ( ∞ ) will be replaced by T r (Room Temperature), T 0 = will be replaced by T l (Temperature of last node).

Discretization of the governing differential equations for the transient heat transfer analysis

Transient thermal analysis is more important than the steady thermal analysis, as this analysis include the variable ambient condition with time. In transient heat conduction, the temperature changes with time as well as position. The finite difference solution of transient heat conduction requires discretization in time in addition to space, as shown in figure-6.

The nodal points and volume elements for the transient FDM formulation of 1-D conduction in a plane wall exist as shown in the figure-7.

For this case the FDM explicit solution for equation (1) will be as follows,

The above equation can be solved explicitly for the temperature ( T m i + 1 ) to give

where,

and

here, τ represents the cell Fourier no, α represents thermal diffusivity, c p represents specific heat at constant pressure, Δ t represents time step, Δ x represents space step.

Above equation is valid for all interior nodes and to find the relation for first and last node, apply boundary conditions (as applicable) as discussed in steady state heat transfer. For a convective & radiation boundary if solar radiation data q s o l a r , in ( ( W / m 2 ) ) is available and absorptivity-transmissivity constant K is known, the relation for temperature is obtained as follows;

Note: the thermal analysis for the roof and floor of a building can be done in same way, as discussed for walls.